Classical field

Definition

See Classical Field Theory .
See gauge theory#Coming from Classical field theories.

A classical field theory is the following data:

• A $n$-dimensional manifold (space-time) $M$,
• A target space $V\cong {\mathbb{R}}^m$, to construct the space of fields $\mathcal{F}=\text{Maps}(M,V)$.
• A Lagrangian, which is a polynomial $L(\varphi ,{\partial }_I\varphi )$, for $|I|\le s\in \mathbb{N}$, where $\varphi \in \mathcal{F}$.
  Then, they are generalized to gauge theories, which are the same stuff but instead of $\mathcal{F}=\text{Maps}(M,V)$ we use sections of a fiber bundle $E\to M$ as matter fields.

Types of fields

• Scalar fields. Section of a rank 1 vector bundle over spacetime. Related to spin 0 particles.
• Vector fields. Section of a rank $n+1$ vector bundle over a $(n+1)$-dimensional spacetime. Related to spin 1 particles.
• Spinor fields (classical spinor field?). When they say a particle has spin 1/2 what they mean is that the particle is the quantum version of a classical spinor field, that is, for every point $p$ in the (3+1)-spacetime we have a vector $v_p$ in such a way that if we consider a change of local frame in $p$ through an element $\varphi \in SO(1,3)$, then $\varphi$ acts on $v_p$ by means of a spin representation of $SO(1,3)$.

Transformations of fields

Given a field, in the sense of an element $\varphi \in \mathcal{F}$, we can consider a diffeomorphism $F:M\to M$ and define a new field $\tilde{\varphi }=F^{\ast }\varphi$, i.e.,

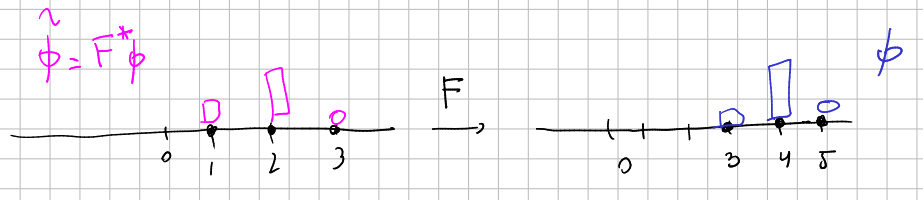
In the picture it looks like if the transformation $F$ is pushing the points of $M$ two units right, but the corresponding transformation of $\varphi$ consists of pushing the field two units left.

Physically, this would be possible if we are transforming the space but not the source of the field. That is, we are changing the relative positions of elements of the universe, not the entire universe.

Usually, $F$ is an element of a local group of transformations of $M$, depending on parameters.

Examples: Consider $M=\mathbb{R}$, and the family of diffeomorphisms $F_{ϵ}:M\to M$ given by $F_{ϵ}(x)=x+ϵv$, where $v\in \mathbb{R}$. Then, the transformation of a field $\varphi$ is given by

Usually, physicist distinguish between active and passive transformations. Let's delve into this. Observe the diagram:

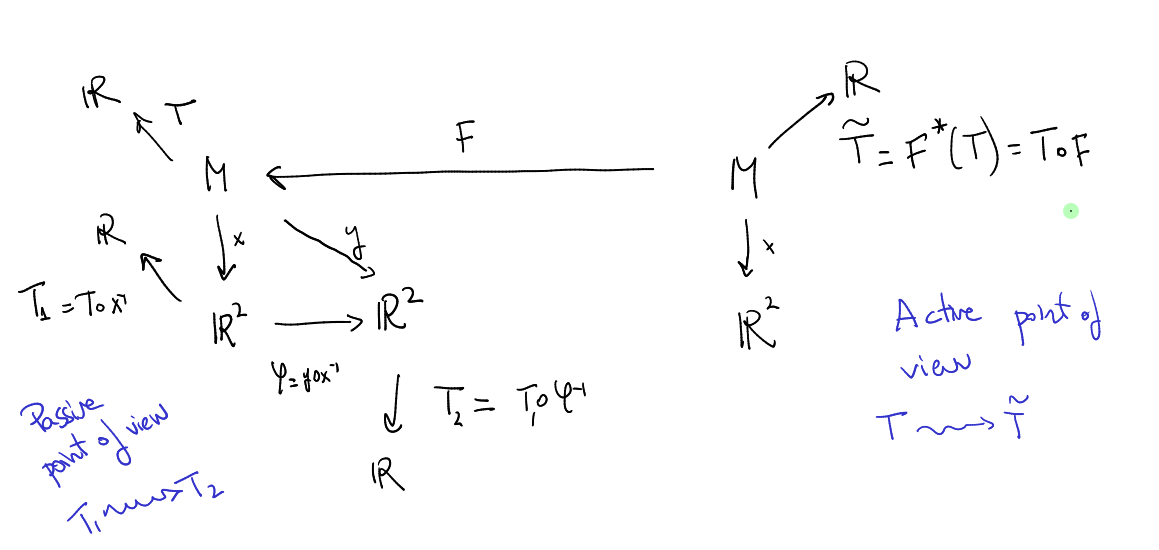
We consider a space $M$ where a field $T$ is defined. In the left side of the diagram, we see that we can express $M$ in two different coordinate systems, given by the maps $x$ and $y$. So we have the corresponding maps $T_1$ and $T_2$, which are usually called "fields" by physicist, by abuse of language (since the real thing is $T$!). The map $\phi :=y\circ x^{-1}$ is a change of coordinates, and we have that $T_1={\phi }^{\ast }(T_2)$. They say that this map is a passive transformation of $T_2$ into $T_1$.
On the other hand, in the right hand side we can see a map $F$ coming from $M$, i.e., a transformation of $M$ into $M$. You can think of $F$ as a counterclockwise rotation, for visualization, if $M$ were a plane space. This transformation let us define a new field (now this is really a new field!) by means of $\tilde{T}:=F^{\ast }(T)$. Physicists calle it an active transformation. It is produced because we are rotating the space $M$ but not the source of the field $T$. Alternatively, we can think as if we were transforming the source of the field with the opposite transformation.

Once we fix a coordinate system for the space, changes of coordinates and proper transformations of $M$ can be interchanged, as we can visualize in the following diagram:

In this sense, a passive transformation can be understood as an active transformation, whenever a coordinate system is distinguished.