Four-current

Related: this video.
CAVEAT: In what follows is not correct to use mass (in the sense of energy) when we go to relativistic context, since what is REAL in SR is the four-momentum, not the mass. All the reasoning below should be done with charges, instead of masses.

Electromagnetic effects happens because of the existence of moving particles with charge. We can imagine that we have infinite charged particles, and their movement being described by infinite curves. But this is not the optimal way to think of them.

First of all, recall that when we study a really large number of mass particles in Classical Mechanics is better to pass to Continuum Mechanics. This way, we substitute a huge number of positions by a distribution of mass density (a 3-form, if we are in 3D space). We count how many particles are in a infinitesimal cube centered at $(x, y, z)$ and construct the differential form

ω = ρ (x, y, z) d x d y d z

that let us recover the mass which is enclosed by a volume $V$ by means of

\int_{V} ρ (x, y, z) d x d y d z

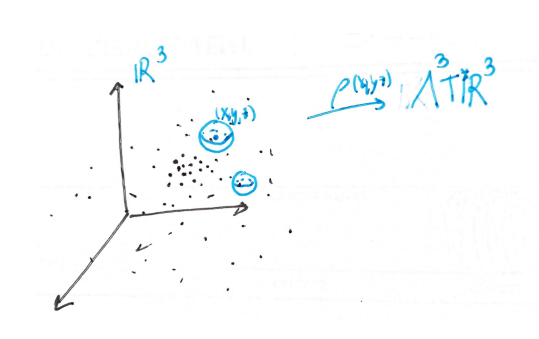
Pasted image 20220415190540.png

In what follows, we will work with two spatial dimensions, to get clearer pictures. So we have a mass density

ω = ρ (x, y, t) d x d y

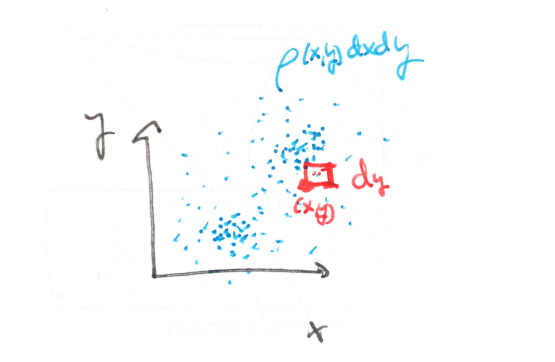
Pasted image 20220415190617.png
(observe we have made our density depends on time, by the way).

But this is not the whole story. Because although we let 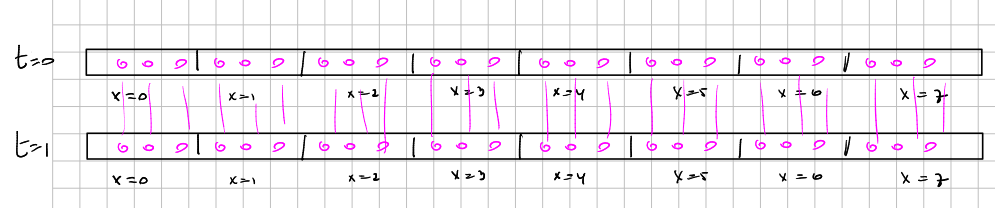$ρ$ depends on $t$ , this does not capture the movement of the infinite particles. The differential form $ω$ only tell us how many particles are there in the infinitesimal red square in any time $t$ . For example, only with $ρ (t, x, y) d x d y$ we cannot distinguish between a bunch of static particles: Pasted image 20231214072131.png
and moving particles
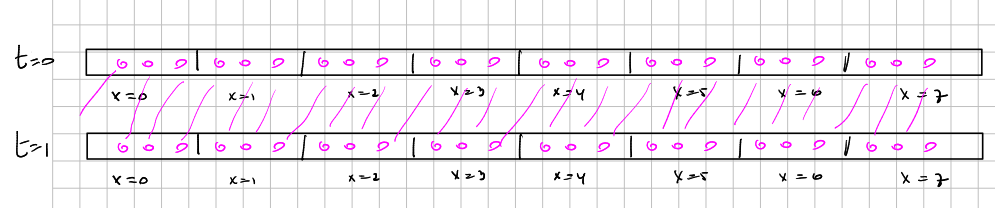
Pasted image 20231214072359.png
So we must include three new quantities to code directions: $j_{x}$ , $j_{y}$ and $j_{z}$ . Let's speak about $j_{x}$ , the others are analogous: it represents the number of particles that pass through an infinitesimal segment ( $d y$ in the picture below) in an infinitesimal amount of time $d t$ . If we pass to a spacetime diagram, we observe that we are speaking about something totally analogous to the density, but instead of a pure spatial window (the square $d x d y$ ) we look at a spacetime window $d y d t$
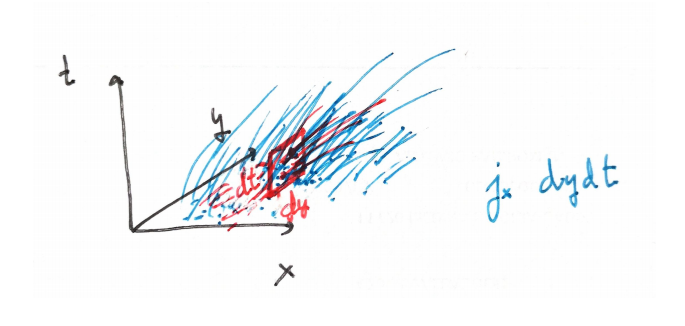
Pasted image 20220415190700.png
This points to the ideas of special relativity, which treats space and time on an equal footing. In fact, we can collect them all in a 4-vector $J = (j_{x}, j_{y}, j_{z}, ρ)$ that transforms well according to Lorentz transformations. It is called the four-current or 4-current. Update: indeed it is a 1-form, see @needham2021visual page 403.

If we use charge instead of mass, we can perform the same analysis. In this case $ρ$ is called charge density and $j = (j_{x}, j_{y}, j_{z})$ is called current density. Just as mass is data that determines the behavior of a system when gravity acts, $ρ$ and $j$ are data to specify the electromagnetic field.

If we assume that no charge can disappear from one place and appear into another without going through the wall of the laboratory (local charge conservation) we get the continuity equation

\partial_{μ} J^{μ} = 0

or also

\frac{\partial ρ}{\partial t} = - (\frac{\partial j_{x}}{\partial x} + \frac{\partial j_{y}}{\partial y} + \frac{\partial j_{z}}{\partial z})

For more info see The Theoretical Minimum vol 3, page 310 and so on.

Relation to four-momentum

The relationship between the four-current of a mass distribution representing a body $V$ and the four-momentum of the body is central to the formulation of relativistic physics. If we have a body given by a mass distribution $ρ$ or, better said, by a four-current $J$ , then the total four-momentum of the body $V$ is given by

P = \int_{V} J d V .

So four-current is a kind of "four-momentum density".

Example: a single electron

The current density $J (x, t)$ corresponding to a single electron with charge $q = - e$ (where $e$ is the elementary charge) following a trajectory $γ (t)$ can be expressed using the Dirac delta function.
Here's the reasoning:

Charge Density: The charge density $ρ (x, t)$ describes the amount of charge per unit volume at a given point in space and time. For a single point particle located at $γ (t)$ , the charge density is non-zero only at that specific location. We can represent this using the three-dimensional Dirac delta function:

ρ (x, t) = q δ^{(3)} (x - γ (t)) = - e δ^{(3)} (x - γ (t))

Relating Current Density to Charge Density and Velocity: The current density $J$ is related to the charge density $ρ$ and the velocity of the charge carriers $v$ by the equation:

J (x, t) = ρ (x, t) v (t)

Substituting and Combining: Substituting the expression for the charge density into the equation for the current density, we get:

J (x, t) = - e \dot{γ} (t) δ^{(3)} (x - γ (t))