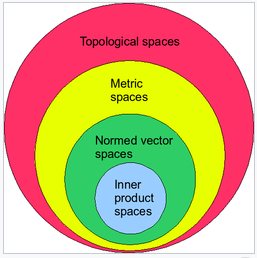
Inner product space

A (real or complex) vector space together with an inner product, i.e., a bilinear form which is:

• non-degenerated. A bilinear form $B$ is called non-degenerate if the following condition holds:
  • If $B(v,w)=0$ for all $w\in V$, then $v=0$.
• conjugate-symmetric
• which is positive-definite.

In the case of $\mathbb{C}$ it is called a Hermitian inner product. In the case of $\mathbb{R}$ is a scalar product or dot product.

If the associated norm gives rise to a topology such that the space is Cauchy complete then it is called a Hilbert space

Identities

• Pithagoras theorem inner product spaces
• Bessel's inequality
• Cauchy-Schwarz inequality
• triangle inequality

Orthonormal basis

They are basis of the vector space which satisfy $⟨e_i,e_j⟩={\delta }_{ij}$.