Laplacian operator

The operator

Δ := \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}

is called the Laplacian operator. It appears in Laplace's equation and in Poisson's equation. Also appears in the heat equation.

It is usually written as $Δ = \nabla^{2} = \nabla \cdot \nabla$ . Also observe that $\nabla \cdot$ is the divergence in the 3D case.

In the 2D case, I understand it like a measure of the "force" existing in every point of a kind of "membrane" due to the influence of the surrounding points. Indeed it is proportional to the mean curvature of the surface, see this.

$Δ u (x, y)$ compares the height at a point with the average of its neighbors.
If $Δ u > 0$ , the point lies below its surroundings → the membrane is pulled upward.
If $Δ u < 0$ , the point lies above its surroundings → the membrane is pulled downward.
Function $f$ has greater absolute value for its Laplacian than $g$ . Both are negative.
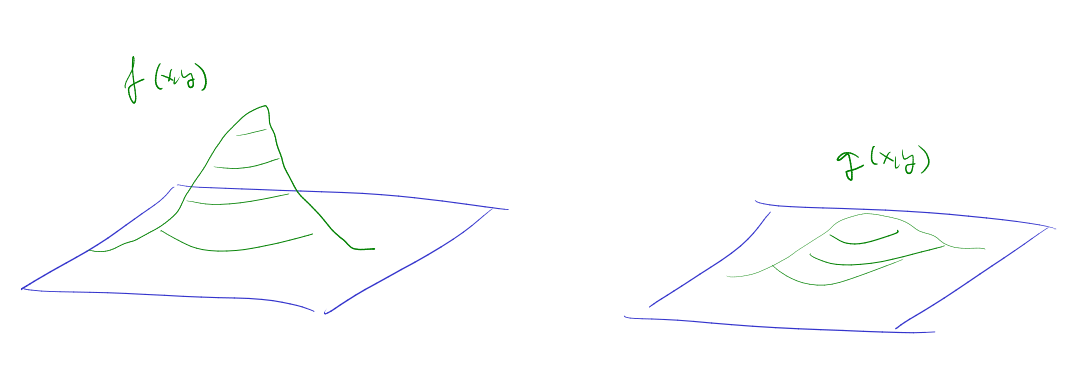
Thus, the Laplacian acts as a restoring force density driving the surface back to equilibrium.
In the wave equation

u_{t t} = c^{2} Δ u,

the Laplacian provides exactly this restoring effect.

On the other hand, harmonic functions are precisely "equilibrium states with respect to this force".