Projections

Given a vector space $V$ , a projection is a map

P : V ⟼ V

such that $P^{2} = P$ .
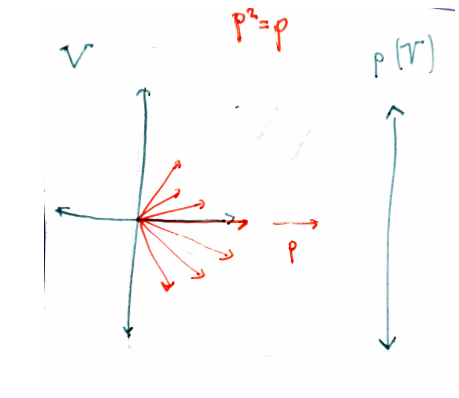
Pasted image 20211017184359.png
Roughly speaking, for a projection you not only need to specify the "target" subspace, but also a "direction" along which to project (the red vectors in the picture above). So, in some sense, a projection gives us a decomposition of the vector space $V$ in horizontal and vertical subspace.

In finite dimensional vector spaces $V$ , the subspaces $U = I m (P)$ and $W = K e r (P)$ satisfies:

$P |_{U}$ is the identity operator.
$V = U \oplus W$ . Every $x \in V$ can be decomposed

x = P x \oplus (x - P x)

Other properties of projections, valid even for infinite dimension, are:

The only eigenvalues allowed for a projection are $0$ and 1, even in complex vector spaces.
The product of two projection is not, in general, another projection. But it is true when they commute.
Even more generally, projections are maps that have a right inverse: $P \circ f = i d_{i m (P)}$

When we work in a Hilbert space $H$ instead of in a plain vector space $V$ , we can say that $P$ is an orthogonal projection if

⟨ P x, y ⟩ = ⟨ x, P y ⟩

that is, if it is a self adjoint operator.
They satisfy the following properties:

Being orthogonal is equivalent to the fact that the image $U$ and the kernel $W$ are orthogonal subspaces: let $u \in U$ and $w \in W$ then $u = P u^{'}$ and $P w = 0$ so

⟨ u, w ⟩ = ⟨ P u^{'}, w ⟩ = ⟨ u^{'}, P w ⟩

Reciprocally, any projection $P$ such that $U$ and $W$ are orthogonal satisfies, assuming $x = u_{1} + w_{1}$ and $y = u_{2} + w_{2}$

⟨ P x, y ⟩ = ⟨ P (u_{1} + w_{1}), u_{2} + w_{2} ⟩ = ⟨ u_{1}, u_{2} ⟩

and

⟨ x, P y ⟩ = ⟨ u_{1} + w_{1}, P (u_{2} + w_{2}) ⟩ = ⟨ u_{1}, u_{2} ⟩

and therefore $P$ is self-adjoint.

Given any closed subspace $U$ of $H$ it there exist an orthogonal projection $P$ such that $i m (P) = U$ . The proof (wikipedia) goes through taking the infimum of the distance...
If $P$ is an orthogonal projection, $I - P$ is an orthogonal projection and

i m (I - P) = K e r (P)

Proof:
First,

(I - P)^{2} = I^{2} - 2 P + P^{2} = I - P

And secondly, $x \in H$ , $(I - P) (x) \in K e r (P)$ since

P (I - P) (x) = P x - P x = 0

$◼$

Orthogonal projections are bounded operators. From Cauchy-Swarth

∥ P v ∥^{2} = ⟨ P v, P v ⟩ = ⟨ P v, v ⟩ \leq ∥ P v ∥ \cdot ∥ v ∥

and so

∥ P v ∥ \leq ∥ v ∥

This is similar, in some sense, to saying that is continue.

Matrix Representation of Orthogonal Projections

Let’s start with the simplest case, where the subspace $i m (P) = U \subset H$ has dimension 1. Let $u \in H$ be a unit vector, i.e., $∥ u ∥ = 1$ , and we want to project vectors onto the line spanned by $u$ .
Then the orthogonal projection of any vector $x \in H$ onto the subspace $U = span {u}$ is:

P (x) = ⟨ u, x ⟩ u

This can be written compactly as:

P = u \cdot u^{*}

or, in Dirac notation:

P = | u ⟩ ⟨ u |

Here:

$| u ⟩$ is the column vector representing $u$ ,
$⟨ u |$ is the row vector (or the conjugate transpose of $u$ ),
The operator $| u ⟩ ⟨ u |$ maps any $x \in H$ to $⟨ u, x ⟩ u$ .
So this formula represents the projection operator onto the subspace spanned by $u$ .
This correspond to the matrix multiplication

(\begin{matrix} a \\ b \\ c \end{matrix}) \cdot (\begin{matrix} a & b & c \end{matrix})

Now, suppose we have a k-dimensional subspace $U \subset H$ , and we choose an orthonormal basis ${u_{1}, u_{2}, \dots, u_{k}}$ for $U$ .
Let’s form a matrix $A$ whose columns are the basis vectors:

A = [\begin{matrix} | & | \\ u_{1} & \dots & u_{k} \\ | & | \end{matrix}] (an n \times k matrix)

Note: Each $u_{i} \in H ≅ C^{n}$ (or $R^{n}$ ).

Then the orthogonal projection operator $P$ onto $U$ is given by:

P = A A^{*}

The intuition is:

$A^{*}$ projects a vector $x \in H$ into the coordinates in the subspace $U$ using the orthonormal basis ${u_{i}}$ .
$A$ then maps those coordinates back into the original space as a linear combination of the basis vectors.