Shannon entropy

Continuous case: differential entropy.

Given a discrete probability distribution $(p_{1}, p_{2}, \dots, p_{n})$ , the Shannon entropy measures the expected information content:

H = - \sum_{i} p_{i} \log_{2} p_{i} .

It quantifies the uncertainty or randomness in the distribution. A higher entropy indicates a more uniform (less predictable) distribution. In a sense, is the "surpriseness" of a probability distribution.
In the discrete case, $H = 0$ means the distribution is fully deterministic.

According to Maldacena in this video it is a measure of the missing information in a message. For example, the sentence "Maria was preparing..." can have different continuations. But "Maria was preparing the dinner" is closed. The first one has entropy.
Formally, this “missing information” corresponds to the probability distribution over possible continuations of the message: when many continuations are plausible with comparable weights, the entropy is high; when the continuation is essentially fixed, the entropy is low (ideally zero). Thus Maldacena’s description is an intuitive restatement of Shannon’s definition, where entropy quantifies the uncertainty in which outcome (or continuation) will occur.

Entropy and guessing games

In a guessing game ("Wordle" or "Guess who", for example), we have a space of answers $S_{0}$ , which has a certain measure $μ$ . For example, the list of 5-letters words or the list of characters, whose measure is obtained by counting.
In each stage of the game we say we gain some information, meaning that we reduce the space of possible answers to a smaller subset of $S_{1} \subseteq S_{0}$ . The information is quantified by the formula

I = - \log_{2} \frac{μ (S_{1})}{μ (S_{0})} .

For example, if we obtain information to reduce the uncertainty area to one half, we say we have obtained 1 bit

I = - \log_{2} \frac{1}{2} = 1.

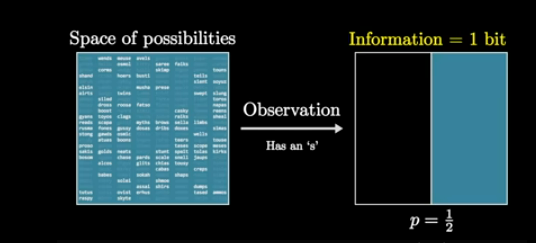
Pasted image 20250821160743.png

For that purpose we make a guess, a question, which induces a partition in the space $S_{0}$ . The other player, or the compute, tell us to what partition does the answer belong. The quality of our guess, i.e., the quality of the partition ${A_{i}}$ , is given by the expected value of the information obtained from it, that is, the entropy, given by

H = \sum_{i} p_{i} (- \log_{2} p_{i}),

where $p_{i} = \frac{μ (A_{i})}{μ (S_{0})}$ . Observe that we are assuming all the final answers have the same probability, so the probability of belonging to an element of the partition is calculated simply by Laplace rule. Underlying this idea is the principle of maximum entropy, I think.

The central challenge in games like "Wordle" or "Guess Who?" is to acquire a specific amount of information while being constrained by the types of questions you're allowed to ask. At the heart of any guessing game is one ultimate, "master question" that would solve it instantly. For "Guess Who?", this question is "Which of the N characters is it?"

This question creates the most granular partition possible, where each of the $N$ possible answers is its own unique subset. The informational value of this question is its entropy, calculated as:

H_{master} = - \sum \frac{1}{N} \log_{2} \frac{1}{N} = \log_{2} (N)

This value represents the total information required to win the game. For a 24-character board, this is $H = \log_{2} (24) \approx 4.585$ bits. This quantity is also known as the initial entropy of the game state, as it measures our total uncertainty at the start.

The crucial rule of the game is that this master question is forbidden. The entire game is about substituting this single, powerful question with a series of smaller, less informative (but legal) questions.

For a mathematical proof that the minimum average number of binary questions required to determine an outcome of a random variable $X$ is between $H$ and $H + 1$ see "Cover, T. M. and Thomas, J. A. (1991), Elements of Information Theory".