Backpropagation

In the context of neural networks, backpropagation is a method for computing the gradients of the loss function with respect to the weights of the neural network, and gradient descent (or its variants) then uses these gradients to update the weights by taking a small step in the direction of the negative gradient, with the goal to arrive at a minimum.

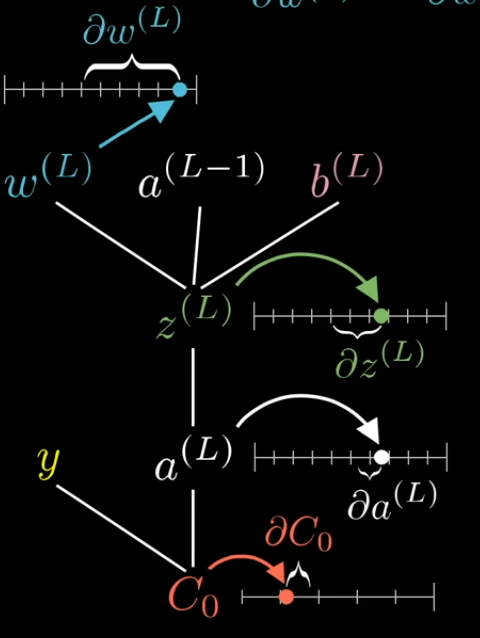
One neuron per layer

From this video
Pasted image 20250504100849.png|300

C_{0} = {(a^{(L)} - y)}^{2}

a^{(L)} = σ (z^{(L)})

z^{(L)} = w^{(L)} a^{(L - 1)} + b^{(L)}

\frac{\partial C_{0}}{\partial w^{(L)}} = 2 (a^{(L)} - y) \cdot σ^{'} (z^{(L)}) \cdot a^{(L - 1)}

Two neurons per layer

C_{0} = (a_{1}^{(L)} - y_{1})^{2} + (a_{2}^{(L)} - y_{2})^{2}

a_{i}^{(L)} = σ (z_{i}^{(L)})

\begin{aligned} z_{1}^{(L)} & = w_{11}^{(L)} a_{1}^{(L - 1)} + w_{12}^{(L)} a_{2}^{(L - 1)} + b_{1} \\ z_{2}^{(L)} & = w_{21}^{(L)} a_{1}^{(L - 1)} + w_{22}^{(L)} a_{2}^{(L - 1)} + b_{2} \end{aligned}

\Rightarrow z^{(L)} = W^{(L)} \cdot A^{(L - 1)} + B

To compute

\frac{\partial C_{0}}{\partial w_{12}^{(L)}},

we need to follow the chain rule for derivatives through the layers of the network.

$C_{0} = (a_{1}^{(L)} - y_{1})^{2} + (a_{2}^{(L)} - y_{2})^{2}$
$a_{i}^{(L)} = σ (z_{i}^{(L)})$
$z_{1}^{(L)} = w_{11}^{(L)} a_{1}^{(L - 1)} + w_{12}^{(L)} a_{2}^{(L - 1)} + b_{1}$
Note that $w_{12}^{(L)}$ only affects $z_{1}^{(L)}$ , so it only influences $a_{1}^{(L)}$ and thus only the first term of the cost.

\frac{\partial C_{0}}{\partial w_{12}^{(L)}} = 2 (a_{1}^{(L)} - y_{1}) \cdot σ^{'} (z_{1}^{(L)}) \cdot a_{2}^{(L - 1)}