Interpretation of complex integration

Ideas in [[alternative complex integration.pdf]] and this video of mine.

Complex integration provides a method for reconstructing a holomorphic function based on its local transformation properties. This approach relies on extending a fundamental geometric fact from basic planar geometry to the complex plane distorted by a function.

The Geometric Foundation

In the complex plane, any final vector $z$ (or $\gamma (1)$) resulting from a curve $\gamma$ is equivalent to the sum of all small tangent vectors along that curve.

• If $\gamma$ maps the interval $[0,1]$ to the complex plane ($\mathbb{C}$), the endpoint $z$ is approximately the sum of vector differences along a partition of the curve.
• In the limit, this sum becomes the integral of the tangent vectors: $$z \approx \sum \gamma(t_{i+1})-\gamma(t_i)\approx \int_0^1 \gamma'(t) dt$$.
  

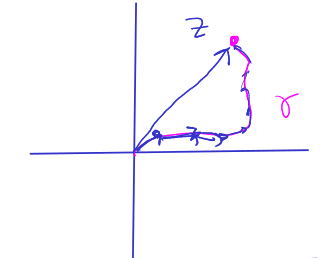
When a holomorphic function $F$ is applied, it "distorts" the complex plane and the curve $\gamma$.

• The distorted vector $F(z)$ remains the sum of the mini tangent vectors of the new curve $F(\gamma )$.
• The relationship between transformed endpoint and the transformed tangent vectors of the new curve is expressed via the integral: $$F(z)\approx \sum F(\gamma(t_{i+1}))-F(\gamma(t_{i+1}))\approx\int_0^1 F'(\gamma(t)) \cdot \gamma'(t) dt.$$
  

Local Transformation: Ampli-Twist

Observe that $F^{\prime }(z)$ contains, as it is well-known, the information on how to rotate and expand (ampli-twist) the neighbourhood around $z$. See Cauchy-Riemann equations.
In other words,

• $F^{\prime }$ measures the local transformation applied by $f$ at each point. Specifically, $F^{\prime }$ measures the rotation (twist) and homothety (amply) applied by the transformation $F$.
• This combination of rotation and expansion is sometimes referred to as an ampli-twist (Needham @Needham1997Visual).
• To construct the transformed vector, $F^{\prime }$ applies the necessary ampli-twist to each tangent vector of the original curve, converting it into the corresponding tangent vector of the transformed curve.

Complex Integration as Reconstruction

The objective of complex integration is to reverse this process: given a function $f$ (representing the collection of local ampli-twists/rotations and homotheties), can we reconstruct the primitive function $F$ from which it came?

The natural method for reconstruction involves defining a potential primitive function $F$ (which depends a priori on the chosen curve $\gamma$). For a point $z\in \mathbb{C}$,

1. Choose an arbitrary curve $\gamma$ starting at a fixed point (e.g., $0$ or $a$) and ending at $z$.
2. Apply the local description $f$ (the required rotation and amplification) to each segment of the curve.
3. Sum the results (performing the Riemann sum/integral) to reconstruct $F(z)$.
4. The construction is written as $F_{\gamma }(z)={\int }_0^{1}f(\gamma (t))\cdot {\gamma }^{\prime }(t)dt$. This is conventionally notated as the integral over the curve $\gamma$, ${\int }_{\gamma }f$.

If the curve $\gamma$ starts at a point $a$, the result of the integration yields $F(z)-F(a)$.

The Failure: Curve Dependence

For complex integration to yield a well-defined primitive function, the result of the integral must not depend on the specific curve $\gamma$ chosen between the fixed starting point and the endpoint $z$.

• If the result is independent of the curve, then the function $F$ is well-defined and we have a "reasonable integration".
• If the result does depend on the curve, there is no primitive function $F$ holomorphic across that entire region.

Example: $f(z)=1/z$ and the Logarithm

Consider the function $f(z)=1/z$. If two different curves (${\gamma }_1$ and ${\gamma }_2$) connect the same start and end points, the integral ${\int }_{\gamma }1/z$ may yield different results.

• In this situation, $1/z$ does not come from a function holomorphic across the entire region; it is related to the logarithm, which requires careful branch definitions.
  See this video of mine.

Geometric Resolution via Riemann Surfaces

The reason seemingly identical endpoints yield different integral values is visualized by considering the Riemann surface corresponding to the transformation (in this case, the logarithm).

• The underlying domain is not simply the complex plane, but a spiral-like structure.
• Moving along different paths in the projection of the complex plane leads to different "levels" or "floors" on the Riemann surface. For instance, moving along ${\gamma }_1$ might lead to one level, while ${\gamma }_2$ causes the path to wrap around and arrive at a different level.
• Crucially, the local description provided by $1/z$ (the giro and homothety instructions) is the same regardless of which "level" or "copy" of the branch cut you project onto the complex plane. The local behavior is uniform.
• This inherent structure leads to the definition of the logarithm naturally being the integral of $1/z$ along a curve $\gamma$ connecting a fixed point to $z$.

Related: Cauchy--Goursat theorem