Solution space of ODEs

In the context set here for ODEs, solutions can be understood as integral curves of the vector field $A$. Using terminology of moving frames of Olver, we can consider the local group of transformations given by the vector field $A$, and the cross section $K=\{(x,u^{(m-1)})\in J^{m-1}:x=0\}$. The fundamental invariants of the solutions are nothing else than the "inicial conditions": $c_0,c_2,\dots ,c_{m-1}$, which constitute a "space" (not necessarily a manifold, maybe an orbifold?) of dimension $m$.

In the case of a homogeneous linear ODE, the solution space constitute a vector space. It is easy to check that the space of fundamental invariants has also the structure of a vector space, an the dimension is $m$, of course.

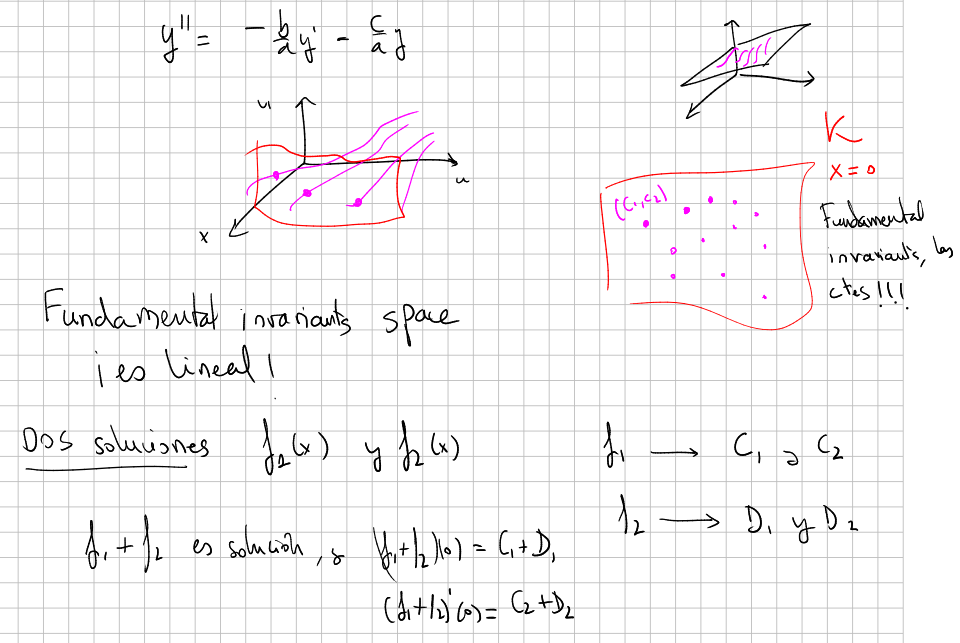
Related with the independence of solutions of a linear ODE is the Wronskian.