Time dilation and length contraction

See this video
It can be shown from the Lorentz boosts.
Helpful case: the muon has a half life, in rest, of $2 μ s$ . Even if it is moving at $0.995 c$ , it is impossible that it arrives to the Earth surface after being created at the atmosphere ( $6500 m$ from the surface). The explanation is due to time dilation or length contraction:
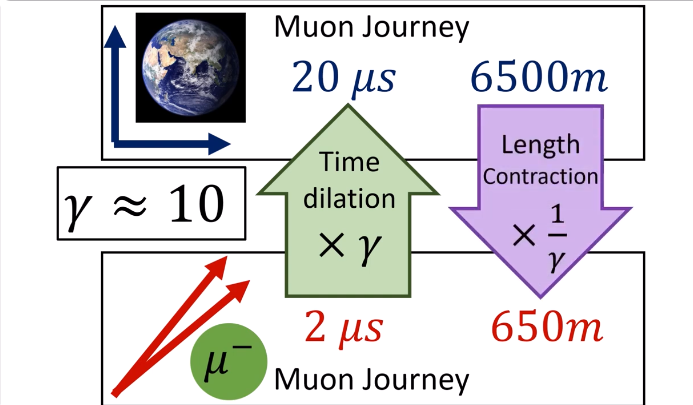
Pasted image 20240705154639.png

Length contraction

Alternative: [[lengthcontraction.pdf]]
Length contraction is not a mechanical compression of an object. Instead, it is a measurement artifact caused by the Relativity of Simultaneity. If two observers cannot agree on "when" the front and back of an object are measured, they cannot agree on "how long" the object is.

The Logic Chain (The "Train" Scenario)

Assume a Moving Observer is on a train and a Standing Observer is on the platform. The Moving Observer wants to measure the train's length ( $L_{0}$ ).

1. The Moving Perspective

The Moving Observer marks the Back and the Front of the train at the exact same time ( $t_{1} = t_{2}$ ). To them, this is a valid measurement of the train's rest length.

2. The Standing Perspective (The Disagreement)

Due to the relativity of simultaneity, the Standing Observer does not see those two marks happen at the same time.

Event A: The Back is marked first.
Time Gap: The train continues to move forward for a split second.
Event B: The Front is marked later.

3. The "Left Behind" Effect

Because the Standing Observer sees the Front being marked after the Back (and after the train has moved), they perceive the Moving Observer's measurement as spanning:

Measurement = Actual Length + Distance Traveled during the time gap

From the Standing Observer's point of view, the Moving Observer measured a distance "longer than it should be" because they included the train's motion in the measurement.

4. Conclusion: Length Contraction

To get the true length of the moving train in the Standing frame, the Standing Observer must measure the Front and Back simultaneously in their own frame. Since the Moving Observer's measurement (which covers $L_{0}$ ) includes that extra "motion distance," the Standing Observer's simultaneous measurement ( $L$ ) must necessarily be shorter.

L < L_{0}

The Measuring Rod (Reciprocity)

Why doesn't the Moving Observer realize this?

The Rod: The measuring rod used by the Moving Observer is also subject to these relativistic effects.
Fair Measure: The Moving Observer thinks they are doing a fair measure because, in their frame, the rod is normal length and the marks are simultaneous.
Standing View of Rod: The Standing Observer sees the Moving Observer using a contracted ruler to measure points at different times.

Summary Formula

The relationship is defined by the Lorentz factor ( $γ$ ):

L = \frac{L_{0}}{γ} = L_{0} \sqrt{1 - \frac{v^{2}}{c^{2}}}

$L$ = Length observed by Standing Observer (Contracted)
$L_{0}$ = Length observed by Moving Observer (Rest Length)
$v$ = Velocity of the train

Relativity: Why Moving Clocks Do Not Tick Slower

Source: this video

The Core Misconception

It is a common misunderstanding in relativity to say that "a moving clock runs slower" or that time physically slows down for moving objects.
This is incorrect. A clock always ticks at its normal rate (1 second per second) in its own reference frame.

The Car Odometer Analogy

Scenario: Imagine two cars driving at the exact same speed (e.g., 100 mph) on a vast plane, but traveling at an angle to each other.
The Measurement: If you are in Car A, looking at Car B "from the side," you observe Car B falling behind your line of motion. You measure Car B's speed relative to your forward direction as slower.
The "Stupid Idea": It would be absurd to claim that Car B's odometer is running slower just because you measure their forward progress as slower.
The Reality: Both odometers accumulate miles at the exact same rate because both cars are actually traveling at 100 mph. The perceived difference is purely due to the angle of their paths.

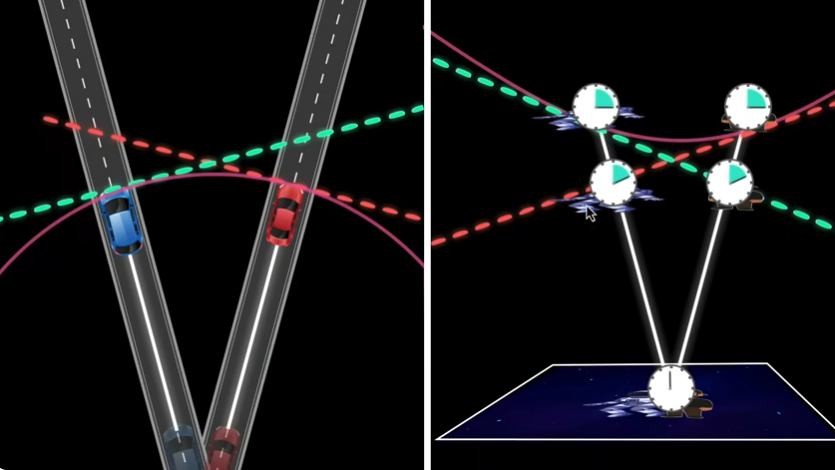
Pasted image 20251231164118.png

Application to Spacetime

This analogy maps directly to Special Relativity:

Motion is an Angle: Moving relative to someone else is equivalent to traveling at an "angle" through 4D spacetime.
Proper Time is the Odometer: The ticking of a clock is the "odometer" of spacetime (measuring Proper Time). Just like the cars, every clock ticks at the same fundamental rate along its own path.
Time Dilation is a Perspective Effect: When we say a moving clock "runs slow," we are merely measuring its path from an angle. Our "line of simultaneity" (what we define as "now") is tilted relative to the moving clock. We are measuring a projection of its time, not the mechanical rate of the clock itself.

Conclusion

Clocks never tick slower.
Time never slows down.
Differences in elapsed time (like in the twin paradox) are not caused by clocks running slow, but by objects taking shorter or longer paths through spacetime.

Note: In the non-Euclidean geometry of spacetime, the straight (inertial) path is the longest duration, while the bent (accelerated) path is shorter.