cinf-structures

Let $\mathcal{Z}=\mathcal{S}(Z_1,\dots ,Z_r)$ be an involutive distribution on a $n$-dimensional smooth manifold $M$. Let $⟨X_1,\dots ,X_{n-r}⟩$ be an ordered collection of independent vector fields and define

for $k=1,\dots ,n-r$; and ${\mathcal{X}}_0=\{Z_1,\dots ,Z_r\}$. We say that $⟨X_1,\dots ,X_{n-r}⟩$ is a cinf-structure for $\mathcal{Z}$ if:

1. ${\mathcal{X}}_k$ is a set of independent vectors for any $p\in M$ and for every $k=1,\dots ,n-r$.
2. The vector field $X_k$ is a ${\mathcal{C}}^{\mathrm{\infty }}$-symmetry of the rank $r+k$ distribution $\mathcal{S}({\mathcal{X}}_k)$, for every $k=1,\dots ,n-r$.

They remind me the idea of flag: we have in $M$ not only a smooth field of $k$-planes (a distribution), but a smooth field of flags.

${\mathcal{C}}^{\mathrm{\infty }}$-structures can be described from a dual point of view, i.e., by means of 1-forms $⟨{\omega }_1,\dots ,{\omega }_{n-r}⟩$.

La existencia de una ${\mathcal{C}}^{\mathrm{\infty }}$-structure permite encontrar las integral submanifolds de la distribución mediante la resolución de Pfaff equations.

Shorter definition
An ordered collection of vector fields $⟨X_1,\dots ,X_m⟩$ is a cinf-structure for the involutive distribution $\mathcal{Z}=\mathcal{S}(Z_1,\dots ,Z_r)$ if the distribution

has constant rank $i+r$ and it is involutive for $1\le i\le m$.
$◼$

Visual scheme for the coefficients of a cinf-structure

The brackets of the vector fields $\{Z_i,X_j\}$ can be seen with the following picture (see [xournal 128]):

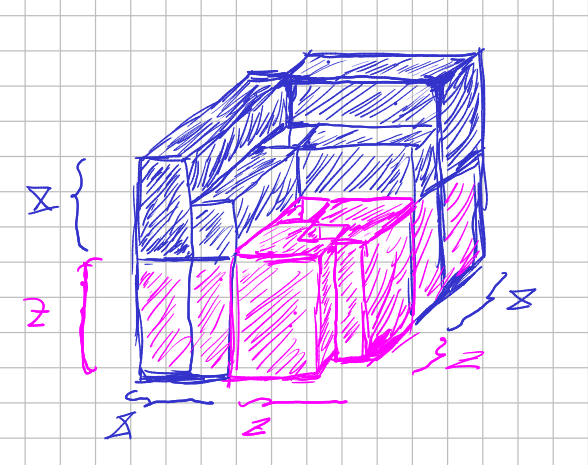
If the cinf-symmetry of distribution are in evolutionary form (in the sense of shuffling symmetries) the picture would be

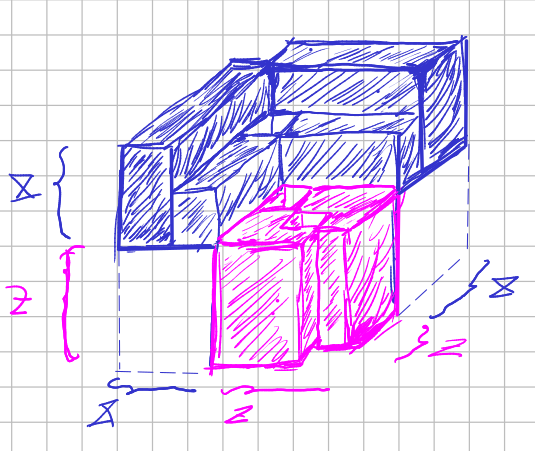
In the case of an ODE and a lambda-symmetry in canonical form the picture would be :

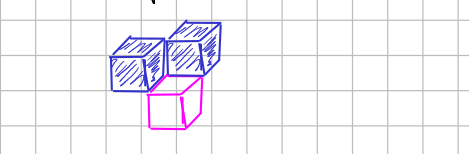
And for an ODE with a cinf-structure in diagonal form (that is, $X_1={\partial }_u+\dots ,X_2={\partial }_{u_1}+\dots ,X_3={\partial }_{u_2}+\dots ,$ and so on) the picture, I think, would be. UPDATE: I THINK THIS IS WRONG!

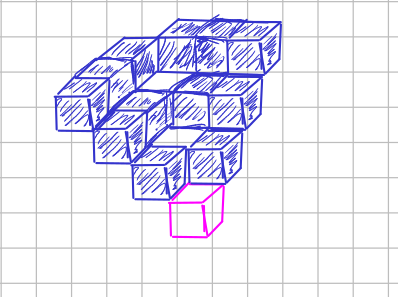
These pictures are the same for the cinf-structure of 1-forms. You have to take into account the result in the note coframe on a manifold that relates the brackets of the frame with the exterior derivative of the coframe.

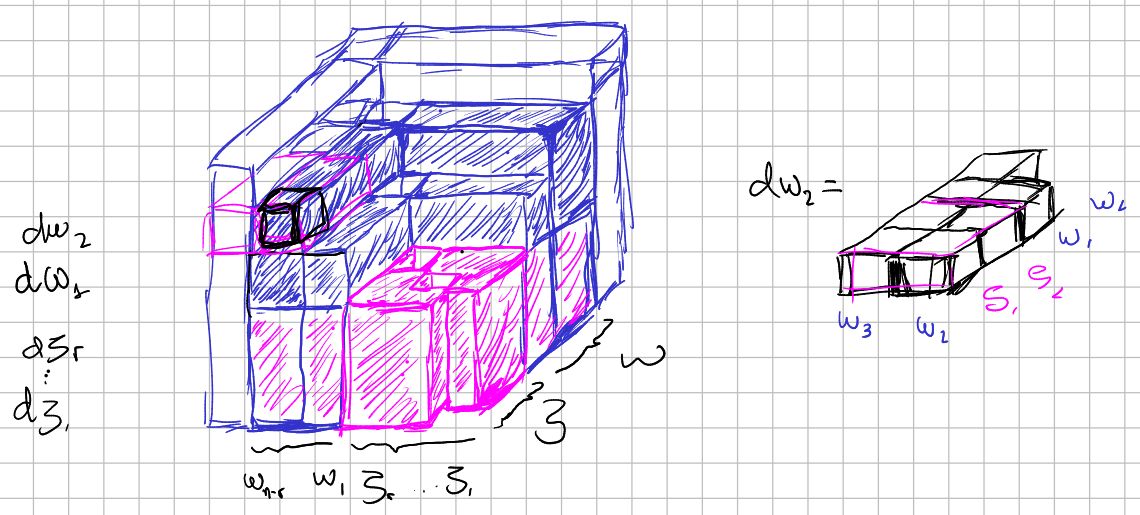
For the coefficients see also [xournal 129] page 2.

See also cinf-structure-based method