Tema 3. Interpolación y aproximación de funciones

1. Introducción

En muchas ocasiones, tras realizar medidas experimentales, obtenemos una tabla de datos para una función en la forma:

x	y
$x_{1}$	$y_{1}$
$x_{2}$	$y_{2}$
$x_{3}$	$y_{3}$
⋮	⋮
$x_{n}$	$y_{n}$
Frecuentemente, necesitamos más información de la función:

Aproximación analítica.
Estimación de derivadas en los puntos conocidos.
Estimación del valor de la función en puntos no tabulados.

En este tema, veremos algunos métodos básicos para determinar estas aproximaciones.

2. Diferencias Divididas de Newton

Una forma de calcular el polinomio de menor grado que pasa por una serie de puntos dados es plantear un sistema de ecuaciones lineales.

Una forma rápida de obtenerlo es usar la fórmula del polinomio de Lagrange. El principal inconveniente de la fórmula de Lagrange es que si añadimos un nuevo punto $(x_{n + 1}, y_{n + 1})$ a nuestra tabla, es necesario recalcular el polinomio desde el principio.

Por eso vamos a estudiar mejor el método de las diferencias divididas de Newton. Partimos de un conjunto de puntos de la forma:

{(x_{1}, y_{1}), (x_{2}, y_{2}), (x_{3}, y_{3}), \dots, (x_{n}, y_{n})}

y definimos:

Diferencias divididas de orden 0: $d_{i} = y_{i}, i = 1, 2, \dots, n .$
Diferencias divididas de primer orden: $d_{i, i + 1} = \frac{d_{i + 1} - d_{i}}{x_{i + 1} - x_{i}} = \frac{y_{i + 1} - y_{i}}{x_{i + 1} - x_{i}}, i = 1, 2, \dots, n - 1.$
Diferencias divididas de segundo orden: $d_{i, i + 1, i + 2} = \frac{d_{i + 1, i + 2} - d_{i, i + 1}}{x_{i + 2} - x_{i}}, i = 1, 2, \dots, n - 2.$
Diferencias divididas de orden $n - 1$ : $d_{1, 2, \dots, n} = \frac{d_{2, 3, \dots, n} - d_{1, 2, \dots, n - 1}}{x_{n} - x_{1}}$

El polinomio de interpolación en términos de las diferencias divididas es:

P_{N} (x) = d_{1} + d_{1, 2} (x - x_{1}) + d_{1, 2, 3} (x - x_{1}) (x - x_{2}) + \dots + d_{1, 2, \dots, n} (x - x_{1}) (x - x_{2}) \dots (x - x_{n - 1})

El cálculo de las diferencias divididas puede llevarse a cabo de forma sencilla mediante la construcción de una tabla. Por ejemplo, si tenemos $n = 5$ , la tabla nos quedaría de la siguiente forma:
Pasted image 20250223130645.png
El polinomio de interpolación tiene la forma:

P_{N} (x) = d_{1} + d_{1, 2} (x - x_{1}) + d_{1, 2, 3} (x - x_{1}) (x - x_{2}) + d_{1, 2, 3, 4} (x - x_{1}) (x - x_{2}) (x - x_{3}) + d_{1, 2, 3, 4, 5} (x - x_{1}) (x - x_{2}) (x - x_{3}) (x - x_{4})

Ejemplo

Dados los puntos (1, 2), (3, 3), (4, 2) y (8, 10), se quiere obtener el polinomio interpolador que pasa por ellos. Hallarlo por medio de las diferencias divididas de Newton.
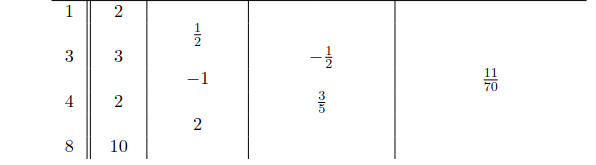
Pasted image 20250223131312.png

P_{N} (x) = 2 + \frac{1}{2} (x - 1) - \frac{1}{2} (x - 1) (x - 3) + \frac{11}{70} (x - 1) (x - 3) (x - 4)

P_{N} (x) = \frac{11}{70} x^{3} - \frac{123}{70} x^{2} + \frac{192}{35} x - \frac{66}{55}

Aproximación de funciones

Otra aplicación de la interpolación de Newton es que nos permite aproximar una función complicada por otra más sencilla. Si tenemos una función $f (x)$ definida en un intervalo $[a, b]$ y elegimos un conjunto de puntos en su gráfica de la forma:

{(x_{0}, f (x_{0})), (x_{1}, f (x_{1})), \dots, (x_{n}, f (x_{n}))}

el polinomio de interpolación de Newton nos proporciona una aproximación de $f$ mucho más sencilla de manejar.

Ejemplo

Dar una aproximación de la función $f (x) = e^{\sqrt{x}}$ con un polinomio que interpole los puntos $0, 1, 4$ y $9$ . Aproximar el valor de $f (3)$ .

Datos:

x: [0, 1, 4, 9]
y: [exp(√0), exp(√1), exp(√4), exp(√9)] = [1.000, 2.718, 7.389, 20.086]

$x_{i}$	$f [x_{i}]$	$f [x_{i}, x_{i + 1}]$	$f [x_{i}, x_{i + 1}, x_{i + 2}]$	$f [x_{i}, x_{i + 1}, x_{i + 2}, x_{i + 3}]$
0.000	1.000	1.718	-0.040	0.018
1.000	2.718	1.557	0.123	-
4.000	7.389	2.539	-	-
9.000	20.086	-	-	-

Polinomio de Newton:

P (t) = 1.000 + 1.718 (t - 0) - 0.040 (t - 0) (t - 1) + 0.018 (t - 0) (t - 1) (t - 4)

Simplificando el polinomio, obtenemos:

P (t) = 0.018 t^{3} - 0.131 t^{2} + 1.831 t + 1.000

Y $P (3)$ =5.804

3. Interpolación de Hermite

En algunas ocasiones, además de los valores de la función, también tenemos el valor de la derivada en los puntos. Es decir, tenemos una tabla de la forma:

x	y	y'
$x_{1}$	$y_{1}$	$y_{1}^{'}$
$x_{2}$	$y_{2}$	$y_{2}^{'}$
$x_{3}$	$y_{3}$	$y_{3}^{'}$
⋮	⋮	⋮
$x_{n}$	$y_{n}$	$y_{n}^{'}$

En este caso, intentamos aproximar la función por un polinomio que satisfaga:

P (x_{i}) = y_{i}, P^{'} (x_{i}) = y_{i}^{'}, i = 1, 2, \dots, n .

Este polinomio recibe el nombre de polinomio de interpolación de Hermite, tiene grado, como máximo $2 n - 1$ , y se calcula de la siguiente manera:

Primera columna: Incluimos los números $z_{i}$ , $i = 1, 2, \dots, 2 n$ definidos como: $z_{2 i - 1} = z_{2 i} = x_{i}, i = 1, 2, \dots, n .$
Segunda columna: Diferencias divididas de orden 0: $d_{2 i - 1} = d_{2 i} = y_{i}, i = 1, 2, \dots, n .$
Tercera columna: Diferencias divididas de primer orden:
Impares

d_{2 i - 1, 2 i} = y_{i}^{'}, i = 1, 2, \dots, n .

Pares
$$
d_{2i,2i+1} = \frac{d_{2i+1} - d_{2i}}{z_{2i+1} - z_{2i}}, \quad i = 1, 2, \ldots, n - 1.
$$

A partir de la cuarta columna: Se construyen como las diferencias divididas de Newton.

El polinomio de Hermite viene dado por:

P_{H} (x) = d_{1} + d_{1, 2} (x - x_{1}) + d_{1, 2, 3} (x - x_{1})^{2} + d_{1, 2, 3, 4} (x - x_{1})^{2} (x - x_{2}) + \dots + d_{1, 2, \dots, 2 n} (x - x_{1})^{2} \dots (x - x_{n - 1})^{2} (x - x_{n})

Ejemplos

Ejemplo 1. Calcular el polinomio de Hermite que interpola la tabla de datos:

$x$	$y$	$y^{'}$
0	1	-1
1	0	1
2	3	-1

Tabla de diferencias divididas:

$x$	$y$	Primera diferencia	Segunda diferencia	Tercera diferencia	Cuarta diferencia	Quinta diferencia
0	1	-1	0	2	-1	-1
0	1	-1	2	0	-3
1	0	1	2	-6
1	0	3	-4
2	3	-1
2	3

Construir el polinomio:
- Usando las diferencias divididas, el polinomio de Hermite es:

P (x) = 1 + (- 1) (x - 0) + 0 (x - 0)^{2} + 2 (x - 0)^{2} (x - 1) + (- 1) (x - 0)^{2} (x - 1)^{2} + (- 1) (x - 0)^{2} (x - 1)^{2} (x - 2)

Simplificando, obtenemos:

P (x) = - x^{5} + 3 x^{4} - x^{3} - x^{2} - x + 1

Ejemplo 2. Un ingeniero aeronáutico está modelando la trayectoria de descenso de un avión antes de aterrizar. Se quiere estimar la altura del avión en función de la distancia hasta el inicio de la pista.
Se tienen las siguientes mediciones:

A 1000 metros antes de la pista, el avión está a 2000 metros de altura, con una velocidad de descenso de -3 m/m (metros por metro recorrido).
A 500 metros antes de la pista, el avión está a 480 metros de altura, con una velocidad de descenso de -2 m/m.
Se pide:
a. Construir el polinomio de interpolación de Hermite que modele la altura del avión en función de la distancia hasta la pista.
b. Usar el polinomio para estimar la altura del avión a 750 metros antes de la pista.

4. Overfitting

El overfitting ocurre cuando un modelo se ajusta demasiado a los datos, capturando ruido y perdiendo capacidad de generalización, lo que suele suceder con polinomios de alto grado que generan oscilaciones no deseadas. Sus causas incluyen el uso de polinomios excesivamente complejos, la presencia de ruido en los datos y una mala extrapolación que conduce a predicciones incorrectas. Para evitarlo, se recomienda usar polinomios de menor grado o splines, elegir nodos de Chebyshev, optar por aproximaciones en lugar de interpolaciones y aplicar regularización para suavizar el modelo, equilibrando así ajuste y generalización.

5. Ejercicios

En una estación de metro pasan convoyes cada 10 minutos durante las primeras horas de la mañana. A las 8:00 suben al convoy 30 personas, 26 a las 8:30 y 21 a las 9:00. Estima (usando el polinomio de interpolación de Newton) cuántas personas suben a las 8:20.
Se considera la función $f (x) = 5^{x}$ .

(a) Utilizar el método de diferencias divididas de Newton para calcular el polinomio de interpolación de los puntos $(- 1, f (- 1))$ , $(0, f (0))$ y $(1, f (1))$ .
(b) Utilízalo para dar una aproximación de $\sqrt{5}$ y calcular el error cometido.

Se consideran los puntos $Q_{1} = (2, 3)$ , $Q_{2} = (4, - 1)$ , $Q_{3} = (6, 4)$ , $Q_{4} = (8, 0)$ y $Q_{5} = (10, - 1)$ .

(a) Calcular el polinomio de interpolación de los puntos $Q_{1}, Q_{2}, Q_{3}, Q_{4}$ usando las diferencias divididas de Newton.
(b) Utilizar las diferencias divididas del apartado anterior para calcular el polinomio de interpolación de los puntos $Q_{1}, Q_{2}, Q_{3}, Q_{4}, Q_{5}$ .

Consideremos la función $f (x) = e^{\sin x}$ .

(a) Utilizar el método de las diferencias divididas de Newton para calcular su polinomio de interpolación en los mismos puntos.
(c) Calcular el error cometido al considerar el valor $p (1.5)$ como aproximación de $f (1.5)$ .

Se considera la función $f (x) = \ln (1 + x)$ .

(a) Calcular el polinomio de interpolación de Hermite en los puntos $x_{1} = 0$ , $x_{2} = 1$ , $x_{3} = 2$ .
(b) Dar una aproximación de $\ln (2.5)$ .

Consideremos la función $f (x) = \frac{x}{1 + x^{2}}$ .

(a) Utilizar el método de las diferencias divididas de Newton para calcular su polinomio de interpolación en los mismos puntos.
(c) Aproximar $f (1.5)$ .

Sea $f (x) = \sin x$ .

(a) Utilizar el método de las diferencias divididas de Newton para calcular su polinomio de interpolación en $x_{0} = 0$ , $x_{1} = \frac{π}{6}$ , $x_{2} = \frac{π}{4}$ , $x_{3} = \frac{π}{2}$ .
(b) Utilizar el polinomio de interpolación de Hermite en los puntos $x_{0}$ y $x_{2}$ .

Sea $f (x) = \cos x$ .

(a) Calcular el polinomio de interpolación de Hermite en los mismos puntos que antes.
(b) Obtener la aproximación del valor $\cos (\frac{π}{4})$ .

Dada la función $f (x) = 2^{1 / x}$ .

(a) Hallar el polinomio de interpolación de $f (x)$ sobre el conjunto de puntos $x_{0} = 0.5$ , $x_{1} = 1$ , $x_{2} = 1.5$ , $x_{3} = 2$ y $x_{4} = 2.5$ , mediante el método de las diferencias divididas de Newton.
(b) Usar dicho polinomio para calcular un valor aproximado de $\sqrt{2}$ . Hallar una estimación del error cometido.

Utilizar el método de Hermite para hallar un polinomio $P (x)$ que satisfaga $P (- 1) = - 1$ , $P^{'} (- 1) = 14$ , $P (2) = 4$ y $P^{'} (2) = 5$ .
Calcular $f (\frac{1}{8})$ a partir de una aproximación de la función $f (x) = \tan (π x)$ con el polinomio de interpolación de Hermite en los puntos $0$ y $\frac{1}{4}$ .
Calcular el polinomio de Hermite que interpola la siguiente tabla:

x	y	y'
-1	5	12
0	2	-7
2	-40	-51