volver al índice

Matemáticas. Ciencias del Mar

Tema 1: Sistemas de Ecuaciones y Matrices

1.1 Sistemas de Ecuaciones

• Se llama sistema de ecuaciones lineales a una colección de ecuaciones lineales que deben ser resueltas simultáneamente.

• Clasificación:

  • Incompatible (SI): Ningún valor de las incógnitas cumple todas las ecuaciones.

  • Compatible Determinado (CD): Hay un único valor.

  • Compatible Indeterminado (CI): Hay infinitos valores.

• Discusión de sistemas (Ejemplo con parámetro $a$):

  • Ecuaciones dadas: $\{\begin{array}{l}x-ay=-2\\ ax-y=2\end{array}$.

  • Al sumar $a$ veces la primera ecuación a la segunda (multiplicando la primera por $-a^2$ y la segunda por $ay=-2a$ en el proceso de eliminación), se llega a la ecuación: $(1-a^2)x=-2-2a$.

  • Casos:

    • $a\ne 1$ y $a\ne -1$ (SCD): El sistema es Compatible Determinado, y la solución para $x$ es: $x=\frac{-2-2a}{1-a^2}$.

    • $a=1$: El sistema se convierte en $\{\begin{array}{l}x-y=-2\\ x-y=2\end{array}$, lo cual es un sistema Incompatible (No es posible).

    • $a=-1$ (SCI): El sistema se convierte en $\{\begin{array}{l}x+y=-2\\ -x-y=2\end{array}$. La segunda ecuación es redundante (múltiplo de la primera), resultando en infinitas soluciones.

• Ejemplo 2 (Sistema con parámetro $a$):

  • Ecuaciones: $\{\begin{array}{l}x+y=20\\ (1+a)x+y=22\end{array}$.

  • Restando las ecuaciones se obtiene: $ax=2$.

  • Casos:

    • $a\ne 0$ (SCD): $x=\frac{2}{a}$ y $y=20-\frac{2}{a}$.

    • $a=0$: El sistema se convierte en $\{\begin{array}{l}x+y=20\\ x+y=22\end{array}$, que es un sistema Incompatible.

1.2 Matrices

• Una de las funciones de las matrices es modelar transformaciones.

  • ${\mathbf{X}}_N=A\cdot {\mathbf{X}}_V$.

  • Para el sistema de ecuaciones: $\{\begin{array}{l}{x}_N=3x_V+2y_V\\ y_N=-4x_V+4y_V\end{array}$.

  • Las matrices vectoriales son ${\mathbf{X}}_N=\left(\begin{array}{c}{x}_N\\ y_N\end{array}\right)$ y ${\mathbf{X}}_V=\left(\begin{array}{c}{x}_V\\ y_V\end{array}\right)$.

  • La matriz de transformación es $A=\left(\begin{array}{cc}3& 2\\ -4& 4\end{array}\right)$.

• Operaciones con matrices:

  • Suma y resta: Triviales.

  • Producto: Cada fila por cada columna.

• Matriz Inversa ($A^{-1}$): Verifica que $A^{-1}\cdot A=I$ (donde $I$ es la matriz identidad).

• Matriz Diagonal: Matriz donde solo los elementos de la diagonal principal son distintos de cero.

Tema 2: Espacios Vectoriales

2.1 Conceptos Básicos

• Un espacio vectorial $V$ es un conjunto con unas operaciones (+ y $\cdot$) que "se comportan de manera natural".

  • Ejemplo: ${\mathbb{R}}^3=\{(x,y,z):x,y,z\in \mathbb{R}\}$.

• Un vector $\mathbf{v}$ es combinación lineal de los vectores $\{{\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3,\dots \}$ si existen números reales ${\alpha }_1,{\alpha }_2,{\alpha }_3,\dots$ tales que $\mathbf{v}={\alpha }_1{\mathbf{u}}_1+{\alpha }_2{\mathbf{u}}_2+{\alpha }_3{\mathbf{u}}_3+\dots$.

• Una colección de vectores es linealmente dependiente si alguno de ellos es combinación lineal de los demás.

• El rango de una matriz es el número de filas o columnas linealmente independientes. Se puede calcular por Gauss.

2.2 Subespacios Vectoriales

• El espacio generado por una colección de vectores $\{{\mathbf{u}}_1,{\mathbf{u}}_2,\dots \}$ es el conjunto de todas sus combinaciones lineales.

• A la colección de vectores se le llama sistema generador de ese espacio.

• Una base de un subespacio es un sistema generador cuyos elementos son linealmente independientes.

• La dimensión de un subespacio $S$ es el número de elementos de una base.

• Un subespacio vectorial $W$ de un espacio vectorial $V$ es otro espacio vectorial $W\subset V$.

  • Ejemplo: $\mathbf{W}=\{(x,y,0)\}$ es un subespacio de ${\mathbb{R}}^3=\{(x,y,z)\}$.

2.3 Formas de Expresar un Subespacio

1. Dando una base.

   • Ejemplo: Base de $W$: $\{(1,1,2),(-1,1,0)\}$.

2. Dando las ecuaciones paramétricas (desde la base).

   $$\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\lambda \left(\begin{array}{c}1\\ 1\\ 2\end{array}\right)+\mu \left(\begin{array}{c}-1\\ 1\\ 0\end{array}\right),\lambda ,\mu \in \mathbb{R}$$$$\{\begin{array}{l}x=\lambda -\mu \\ y=\lambda +\mu \\ z=2\lambda \end{array}$$

3. Dando las ecuaciones implícitas (desde la base).

   • La ecuación implícita para el ejemplo anterior es $-x-y+z=0$.

• De Implícita a Base:

  • Para el sistema $\{\begin{array}{l}x-3y+z=0\\ 2x-y=0\end{array}$ , la solución paramétrica es:

    • $y=\frac{2}{5}z$ y $x=\frac{1}{5}z$.

    • Si se toma $z=5$, se obtiene el vector $\mathbf{u}=(1,2,5)$, que es la base.

Tema 3: Diagonalización

3.1 Contexto

• Se utiliza para calcular ${\mathbf{X}}_F=A^k\cdot {\mathbf{X}}_V$, donde $A$ es la matriz de interacción entre poblaciones.

  • Ejemplo: Para $\bar{x}=3x+y$, $\bar{y}=2x+2y$, la matriz es $A=\left(\begin{array}{cc}3& 1\\ 2& 2\end{array}\right)$.

• La diagonalización es necesaria para simplificar el cálculo de $A^{20}$. La idea es cambiar a unas "series imaginarias A y B que se comportan mejor" (es decir, a un sistema independiente).

3.2 Procedimiento

1. Cálculo de valores propios ($\lambda$): Resolver la ecuación característica $|(A-\lambda I)|=0$.

   • Para $A=\left(\begin{array}{cc}3& 1\\ 2& 2\end{array}\right)$, la ecuación es $(3-\lambda )(2-\lambda )-2=0$, que se simplifica a ${\lambda }^2-5\lambda +4=0$.

   • Los valores propios son ${\lambda }_1=4$ y ${\lambda }_2=1$.

2. Cálculo de vectores propios ($\mathbf{v}$): Para cada $\lambda$, resolver $(A-\lambda I)\mathbf{v}=\mathbf{0}$.

   • Para ${\lambda }_1=4$: $\{\begin{array}{l}-x+y=0\\ 2x-2y=0\end{array}⟹x=y$. Vector propio ${\mathbf{v}}_1=\left(\begin{array}{c}1\\ 1\end{array}\right)$.

   • Para ${\lambda }_2=1$: $\{\begin{array}{l}2x+y=0\\ 2x+y=0\end{array}⟹y=-2x$. Vector propio ${\mathbf{v}}_2=\left(\begin{array}{c}1\\ -2\end{array}\right)$.

3. Construcción de $P$ y $D$:

   • Matriz de paso (vectores propios): $P=\left(\begin{array}{cc}{\mathbf{v}}_1& {\mathbf{v}}_2\end{array}\right)=\left(\begin{array}{cc}1& 1\\ 1& -2\end{array}\right)$.

   • Matriz Diagonal (valores propios): $D=\left(\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right)=\left(\begin{array}{cc}4& 0\\ 0& 1\end{array}\right)$.

   • Se obtiene que $A=PD{P}^{-1}$.

   • La inversa es $P^{-1}=\frac{1}{3}\left(\begin{array}{cc}2& 1\\ 1& -1\end{array}\right)$.

4. Cálculo de $A^{20}$ y ${\mathbf{X}}_F$:

   • $A^{20}=P\cdot D^{20}\cdot P^{-1}=\frac{1}{3}\left(\begin{array}{cc}2\cdot 4^{20}+1& 4^{20}-1\\ 2\cdot 4^{20}-2& 4^{20}+2\end{array}\right)$.

   • Para ${\mathbf{X}}_V=\left(\begin{array}{c}5\\ 2\end{array}\right)$, la solución final ${\mathbf{X}}_F=\left(\begin{array}{c}{x}_F\\ y_F\end{array}\right)$ es:

     $$x_F=5\cdot \left(\frac{2\cdot 4^{20}+1}{3}\right)+2\cdot \left(\frac{4^{20}-1}{3}\right)$$$$y_F=5\cdot \left(\frac{2\cdot 4^{20}-2}{3}\right)+2\cdot \left(\frac{4^{20}+2}{3}\right)$$

Tema 4: Cálculo Diferencial en una Variable

4.1 Límite y Continuidad

• Definición de Límite: Se llama límite de una función $f$ cuando $x$ se acerca a $x_0$ al valor al que se acerca $f(x)$.

• Teorema de Bolzano: Las funciones continuas en $[a,b]$ cumplen que si $f(a)$ y $f(b)$ tienen signo contrario, entonces la ecuación $f(x)=0$ tiene al menos una solución dentro de $(a,b)$.

4.2 Derivada

• La derivada $f^{\prime }(x_0)$ se define como:

  $$f^{\prime }(x_0)=\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}$$

• La derivada es la "inclinación" de la función.

4.3 Extremos y Optimización

• Ejercicio de Extremos: Hallar los extremos de $f(x)=x^3-5x^2+3x+2$.

  • Derivada: $f^{\prime }(x)=3x^2-10x+3$.

  • Los puntos críticos se obtienen de $f^{\prime }(x)=0$, dando como soluciones $x=3$ y $x=\frac{1}{3}$.

  • Análisis (usando la segunda derivada o tabla de signos):

    • $x=\frac{1}{3}$ es un máximo local.

    • $x=3$ es un mínimo local.

• Ejemplo de Optimización (Minimizar gasto de aluminio):

  • Minimizar el área de una lata de 0.33 L.

  • Volumen: $V=\pi r^{2}h=0.33{\text{ dm}}^3$.

  • Área (función a minimizar): $A(r,h)=2\pi r^2+2\pi rh$.

  • Sustituyendo $h=\frac{0.33}{\pi r^2}$, el área solo depende de $r$: $A(r)=2\pi r^2+\frac{0.66}{r}$.

  • Para encontrar el mínimo, se resuelve $A^{\prime }(r)=4\pi r-\frac{0.66}{r^2}=0$.

  • Solución: $r^3=\frac{0.66}{4\pi }$, resultando en $r\approx 0.37\text{ dm}$ y $h\approx 0.76\text{ dm}$.

4.4 Polinomio de Taylor

• La recta tangente es $y=f(a)+f^{\prime }(a)(x-a)$.

• El polinomio de Taylor $P_{n,a}(x)$ de grado $n$ es la generalización de la recta tangente.

• Se calcula mediante la fórmula:

  $$P_{n,a}(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k$$

  que es $f(a)+f^{\prime }(a)(x-a)+\frac{f^{″}(a)}{2!}(x-a{)}^2+\frac{f^{‴}(a)}{3!}(x-a{)}^3+\dots$.

• El polinomio de Taylor para $a=0$ se llama polinomio de Maclaurin.

Tema 5: Derivación en Varias Variables

5.1 Funciones de Varias Variables

• Son funciones que pueden depender de más de una entrada y devolver varios números.

• Ejemplos:

  • $f:{\mathbb{R}}^2\to \mathbb{R}$: Asigna a $(x,y)$ un escalar (e.g., $f(x,y)=x\cdot y$). Se representa gráficamente con curvas de nivel ($f(x,y)=c$), como isobaras (presión) o isotermas (temperatura) .

  • $g:\mathbb{R}\to {\mathbb{R}}^2$: Asigna a $t$ un vector $(x(t),y(t))$ (e.g., longitud y latitud en función del tiempo).

  • $f:{\mathbb{R}}^2\to {\mathbb{R}}^2$: Asigna a $(x,y)$ un vector $(u,v)$ (e.g., el viento $(u,v)$ en cada posición $(x,y)$).

5.2 Derivadas Parciales

• Consiste en derivar de la manera tradicional, pero considerando todas las demás variables como constantes.

• La derivada parcial de $f$ respecto a $x$ ($g_x$) mide la influencia de $\partial x$ en el comportamiento de $f$.

5.3 Gradiente y Derivada Direccional

• El gradiente ($\mathrm{\nabla }f$) es un vector en cada punto que da la dirección de mayor incremento de la función.

  $$\mathrm{\nabla }f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$$

• La derivada direccional ($D_{\mathbf{v}}f$) calcula el incremento de la función en la dirección $\mathbf{v}=(a,b)$:

  $$D_{\mathbf{v}}f=a\frac{\partial f}{\partial x}+b\frac{\partial f}{\partial y}$$

5.4 Rotacional y Divergencia

• Rotacional ($\text{rot}(\mathbf{f})$):

  • Mide la tendencia de un campo de vectores a girar en cada punto.

  • Para un campo $\mathbf{f}:{\mathbb{R}}^2\to {\mathbb{R}}^2$, $\mathbf{f}=(f_1,f_2)$: $\text{rot}(\mathbf{f})=\frac{\partial f_2}{\partial x}-\frac{\partial f_1}{\partial y}$.

  • Para un campo $\mathbf{f}:{\mathbb{R}}^3\to {\mathbb{R}}^3$, $\mathbf{f}=(f_1,f_2,f_3)$, el rotacional es otro campo vectorial:

  $$\mathrm{rot}(\mathbf{f})=\left(\begin{array}{c}{\displaystyle \frac{\partial f_3}{\partial y}-\frac{\partial f_2}{\partial z}}\\ {\displaystyle \frac{\partial f_1}{\partial z}-\frac{\partial f_3}{\partial x}}\\ {\displaystyle \frac{\partial f_2}{\partial x}-\frac{\partial f_1}{\partial y}}\end{array}\right).$$
  • Equivalente a la fórmula mnemotécnica mediante determinante formal con el gradiente ($\mathrm{\nabla }$):
  $$\mathrm{rot}(\mathbf{f})=\mathrm{\nabla }\times \mathbf{f}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ f_1& f_2& f_3\end{array}\right|.$$

• Divergencia ($\text{Div}(\mathbf{f})$):

  • Mide la cantidad de flujo que se crea o se extingue en cada punto.

  • Para un campo $\mathbf{f}:{\mathbb{R}}^2\to {\mathbb{R}}^2$: $\text{Div}(\mathbf{f})=\frac{\partial f_1}{\partial x}+\frac{\partial f_2}{\partial y}$.

  • Para un campo $\mathbf{f}:{\mathbb{R}}^3\to {\mathbb{R}}^3$: $\text{Div}(\mathbf{f})=\frac{\partial f_1}{\partial x}+\frac{\partial f_2}{\partial y}+\frac{\partial f_3}{\partial z}$.

5.5 Optimización en Varias Variables (Extremos Locales)

Para encontrar máximos y mínimos locales:

1. Encontrar puntos críticos: Resolver $\mathrm{\nabla }f=\mathbf{0}$.

2. Calcular la matriz Hessiana ($H$): La matriz de segundas derivadas parciales.

   $$H=\left(\begin{array}{cc}{f}_{xx}& f_{xy}\\ f_{yx}& f_{yy}\end{array}\right)$$

3. Calcular $\text{det}(H)$ para cada punto crítico:

   • Si $\text{det}(H)>0$ y $f_{xx}>0⟹$ Mínimo local.

   • Si $\text{det}(H)>0$ y $f_{xx}<0⟹$ Máximo local.

   • Si $\text{det}(H)<0⟹$ Punto de silla.

   • Si $\text{det}(H)=0⟹$ No se sabe.

Tema 6: Integración

Antiderivadas

...

Cambio de variable

...

Integración por partes

...

Integrales racionales

...

Cálculo de áreas

...

Otras aplicaciones

• Masa dada la densidad (de un alambre)

Integrales dobles

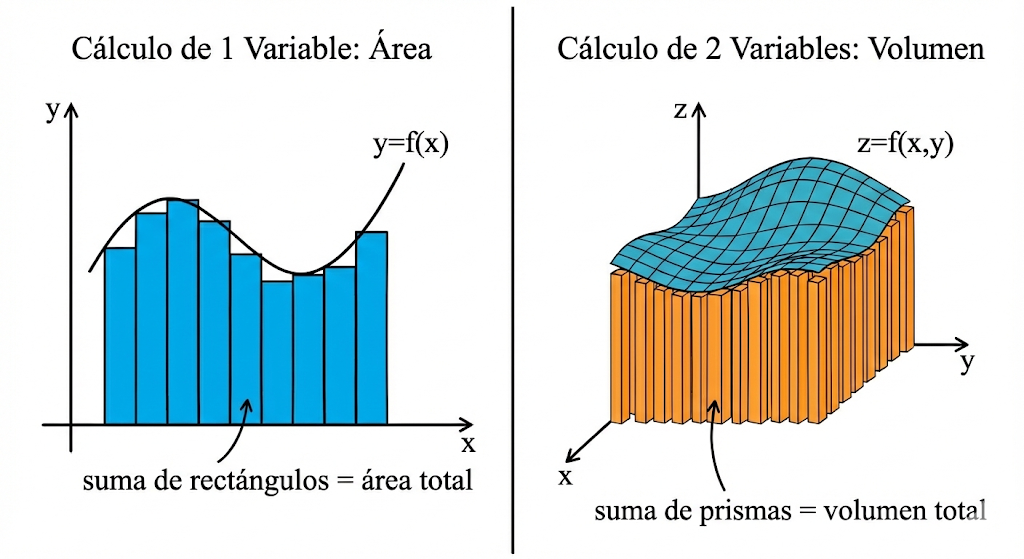
Idea: De manera análoga a cómo en una variable sumamos una infinidad de rectángulos diminutos para calcular el área bajo una curva, en el cálculo de varias variables extendemos este concepto. Con las integrales dobles, sumamos una infinidad de prismas rectangulares infinitesimalmente delgados para determinar el volumen total que se encuentra bajo una superficie.

Teorema de Fubini

Permite calcular integrales dobles como integrales iteradas (o sucesivas).

• Sobre Rectángulos: Si $\mathrm{\Omega }=[a,b]\times [c,d]$:

• Sobre Regiones Generales:
  • Tipo I (Vertical): $\mathrm{\Omega }=\{(x,y)\in {\mathbb{R}}^2:a\le x\le b,g_1(x)\le y\le g_2(x)\}$,

- Tipo II (Horizontal): $\mathrm{\Omega }=\{(x,y)\in {\mathbb{R}}^2:c\le y\le d,h_1(y)\le x\le h_2(y)\}$,

Cambio de Orden de Integración

Consiste en describir una región de Tipo I como una región de Tipo II (o viceversa) para facilitar la integración. Es fundamental dibujar la región de integración.

Aplicaciones

• Área (2D): $A(\mathrm{\Omega })={\iint }_{\mathrm{\Omega }}1dA$
• Volumen bajo superficie: $V={\iint }_{\mathrm{\Omega }}(z_{techo}(x,y)-z_{suelo}(x,y))dA$
• Masa: $M={\iint }_{\mathrm{\Omega }}\sigma (x,y)dA$

Integrales Triples

Se calculan de forma análoga a las dobles, usando el Teorema de Fubini.

• Sobre Cajas Rectangulares: Si $\mathrm{\Omega }=[a,b]\times [c,d]\times [e,f]$:

  $${\iiint }_{\mathrm{\Omega }}f(x,y,z)dV={\int }_a^b{\int }_c^d{\int }_e^{f}f(x,y,z)dzdydx\text{(y los otros 5 órdenes)}$$

• Sobre Regiones Generales: Si $W\subset {\mathbb{R}}^3$ se proyecta sobre una región $\mathrm{\Omega }$ en el plano $XY$, y está limitada superior e inferiormente por $z=u_2(x,y)$ y $z=u_1(x,y)$:

  $${\iiint }_{W}f(x,y,z)dV={\iint }_{\mathrm{\Omega }}({\int }_{u_1(x,y)}^{u_2(x,y)}f(x,y,z)dz)dA$$

Aplicaciones

• Volumen: ${\iiint }_{\mathrm{\Omega }}1dxdydz$
• Masa: $M={\iiint }_{\mathrm{\Omega }}\sigma (x,y,z)dxdydz$