Product in categories

Given two objects $A$ and $B$ in a category, the product is another object $P$ together with two morphisms $π_{1} : P \mapsto A$ and $π_{2} : P \mapsto B$ that satisfy the following universal property: if $X$ is any other object in the category with morphisms $f_{1} : X \to A$ and $f_{2} : X \to B$ then there is an unique morphism $g : X \to P$ such that $f_{1} = π_{1} \circ g$ and $f_{2} = π_{2} \circ g$
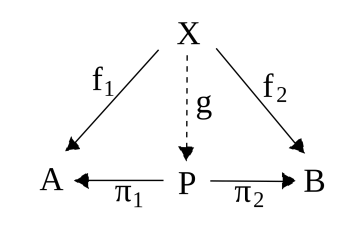
Pasted image 20210928190422.png
When the product exists is unique up to isomorphisms.

Examples

Given the category of sets with morphisms the functions, the product of two sets $A$ and $B$ is the cartesian product $A \times B$ with the natural projection functions.
For a set $S$ the powerset $P (S)$ is a category whose morphisms are the inclusions. The product of two elements $A, B \in P (S)$ is the intersection $A \cap B$
Greatest common divisor and least common multiple are products in their respective categories of partial ordered sets.
In the category of groups, the product is the direct product of groups (versus the semidirect product case)

More comments

The product is associative up to isomorphism, that is, given $A, B, C$ in the category we have

(A \times B) \times C ≅ A \times (B \times C)

The product can be defined for $n$ objects in the category, including $n = 1$ and $n = 0$ . One category in which all the $n$ -products are defined is called a \textbf{cartesian category}.
In fact, the product can be defined for an arbitrary family of objects indexed by a set $I$ :

(X_{i})_{i \in I}

The product would be another object $X$ (usually denoted by $Π_{i \in I} X_{i}$ ) together with a family of morphisms indexed by $I$ ,

π_{i} : X \to X_{i}

satisfying the analogous universal property: for any other object $Y$ and family of morphisms $f_{i} : Y \to X_{i}$ there exists an unique $g : Y \mapsto X$ such that $f_{i} = π_{i} \circ g$

A dual notion is that of coproduct in categories.