Cauchy stress tensor

It belongs to the realm of Continuum Mechanics, but also it is related to the energy-momentum tensor.
Bodies usually have internal forces due to the interactions between their constituent particles. These forces, distributed throughout the material, arise when the body is subjected to external loads, such as forces or displacements, or when there are internal factors like thermal expansion or phase changes. The Cauchy stress tensor is a mathematical model that describes how these internal forces are distributed over a material's surface, offering a detailed account of the internal state of stress at any given point within the body.

It is a $(1, 1)$ -tensor field, so at every point $p$ in the material's manifold $M$ , we have a linear map $σ_{p} : T_{p} M \to T_{p} M$ . Now, if $v \in T_{p} M$ is a vector at the point $p$ , $σ_{p} (v)$ represents the internal force per unit area acting on a hypothetical surface whose normal vector is $v$ .
More specifically, the vector $σ_{p} (v)$ is the stress vector (also called traction vector or force per unit area) acting on that surface. This stress vector describes the direction and magnitude of the internal force that neighboring parts of the material exert on the surface element whose normal is $v$ .

If we choose coordinates we have:

σ = [\begin{matrix} σ_{x x} & σ_{x y} & σ_{x z} \\ σ_{y x} & σ_{y y} & σ_{y z} \\ σ_{z x} & σ_{z y} & σ_{z z} \end{matrix}]

The diagonal elements of the stress tensor ( $σ_{x x}$ , $σ_{y y}$ , $σ_{z z}$ ) represent the normal stresses. These components describe the force per unit area acting perpendicular to the surface element.

$σ_{x x}$ : The normal stress in the $x$ -direction, acting on a surface element with a normal vector pointing in the $x$ -direction.
$σ_{y y}$ : The normal stress in the $y$ -direction, acting on a surface element with a normal in the $y$ -direction.
$σ_{z z}$ : The normal stress in the $z$ -direction, acting on a surface element with a normal in the $z$ -direction.

If these normal stresses are compressive (i.e., acting inward), they are typically associated with pressure or compressive stress

The off-diagonal elements ( $σ_{x y}$ , $σ_{x z}$ , $σ_{y z}$ , etc.) represent shear stresses. These describe the force per unit area acting tangentially to the surface element, leading to a tendency to deform the material by sliding one layer over another.

Examples

Gas in equilibrium

The Cauchy stress tensor $σ$ for a gas in equilibrium can be written as:

σ = [\begin{matrix} - p & 0 & 0 \\ 0 & - p & 0 \\ 0 & 0 & - p \end{matrix}]

where $p$ is the pressure of the gas. Here:

$- p$ appears on the diagonal, representing the compressive normal stress due to the gas pressure.
The off-diagonal elements are zero because, for an isotropic medium like a gas at equilibrium, there are no shear stresses.

One direction tension

Another simple example of a Cauchy stress tensor is that of a uniaxial tensile stress, where a material is stretched along one axis (say, the $x$ -axis) and experiences no stress in the perpendicular directions.
Suppose a metal bar, with all its atoms in equilibrium. Then the Cauchy stress tensor would be

σ = [\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}]

But if the material is subjected to a tensile force along the $x$ -axis, and there is no stress in the $y$ - and $z$ -directions, the stress tensor for this situation looks like:

σ = [\begin{matrix} σ_{x x} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}]

Here:

$σ_{x x} > 0$ represents the tensile stress in the $x$ -direction.
The normal stresses $σ_{y y}$ and $σ_{z z}$ are zero because there is no force in the $y$ - and $z$ -directions.
The off-diagonal components (shear stresses) are also zero since the force is purely normal and there is no sliding between layers of material.

Relation to force experienced by a body element

The Cauchy stress tensor provides information about the internal forces within the material and how they vary across different directions at each point. This allows for the determination of how the material will respond to these forces, leading to its deformation.

The general approach is to use the Cauchy stress tensor in conjunction with the equations of motion (or equilibrium in static cases), which are derived from the balance of linear momentum:

div (σ) + b = ρ a

where:

$σ$ is the Cauchy stress tensor,
$b$ is the external force per unit volume (e.g., gravity),
$ρ$ is the mass density,
$a$ is the acceleration field.

Simulation

See Mathematica 019. But it is wrong...

Old stuff, probably it should be erased

This is a topic that is halfway between Physics and Engineering. We are going to deal, in a very simplistic approach, with how the 3D bodies get deformed, but we will alternate between 3D and 2D for visualization issues. Suppose we have a body that occupies a region of space $Ω$ and suffers a small transformation into a new region $Ω^{'}$ in a very general way, that includes deformation, translation and rotation. We interpret that every particle of the body which in the initial state was in position $x \in Ω$ gets transformed to $T (x) \in Ω^{'}$

T : Ω ⟼ Ω^{'}

If we think of the transformation as being the resulting action of forces applied on the constituent particles of the body, and we assume that these particles were initially at rest (a solid) we can state that the forces in every point $x$ are approximately:

F (x) \approx λ (T (x) - x)

for some constant $λ \in R$
Pasted image 20231213121509.png

This is because we can look at $T$ as the result of a continuous transformation $T_{t}$ depending on a parameter $t$ such that $T_{0} = I$ and $T_{1} = T$ . This way, $α (t) = T_{t} (x)$ is the curve describing the evolution of particle $x$ , and by Taylor expansion we have

T_{1} (x) = x + \frac{d}{d t} T_{t} (x) |_{t = 0} + \frac{1}{2} \frac{d^{2}}{d t^{2}} T_{t} (x) |_{t = 0} + \dots

and since particles were initially at rest

T (x) \approx x + \frac{1}{2 μ} F (x)

where we are assuming, also, that the body has constant density $μ$ .

Studying the whole transformations is complicated, because of nonlinearity. So we should better take care of the local study of every point, assuming that the transformation is very small, as we usually do (it is the same simplification that we do when we pass from studying the curve described by a particle to the tangent vector of that curve). We can imagine that every point $x$ is surrounded by a sphere of very near points $y$ , and we want to know how the latter get transformed. That is, we center our attention over $x$ and $T (x)$ , and watch the relative displacement of the surrounding $y$ s. In the end, this is like saying that a vector $v$ leaving from $x$ is associated with

d F_{x} (v)

since, as we observe in the picture on the right, $v$ is associated with

w = T (y) - (T (x) + y - x) = T (y) - y - (T (x) - x) = F (y) - F (x)

So, what is the physical meaning of $d F_{x}$ ? In the same way that $d T_{x}$ (usually called deformation gradient) describes us the infinitesimal transformation of an infinitesimal piece of the object, $d F_{x} (= d T_{x} - I_{x})$ tells us, in some sense, the contribution to deformation applied to the piece in every direction. This is the precursor of the Cauchy stress tensor. We can think of it like a linear map that tells us how directions get transformed into new directions. That is, the vector that we have to add to every direction to obtain the new one. We will call it deformation force.

But now, since we concern only with deformations, it would be good if we can remove the rotation part (the translation part is removed by derivation), but this is allowed by the polar decomposition. We have that

d T_{x} = R_{x} \cdot U_{x}

where $R$ is a rotation matrix and $U$ is a symmetric matrix called the right stretch tensor, and it contains the relevant information about the pure deformation. Observe that if we had begin with a transformation such that $R_{x} = I$ for our point of interest $x$ , or if we multiply our original transformation by the constant matrix $R_{x}^{- 1}$ , then the matrices $d T_{x}$ and $d F_{x}$ would be symmetric, and therefore, diagonalizable.

So let's assume $d F_{x}$ is symmetric and go back to the physical meaning. If we change to the diagonal basis, the matrix $d F_{x}$ is telling us that in every main direction going out the particle $x$ we are experiencing a "deformation force" (I think that the technical name is stress) parallel to that direction. Something like pressure when we are under water, but not necessarily the same for every direction, and not necessarily inward. The result is a non-symmetric scale change.
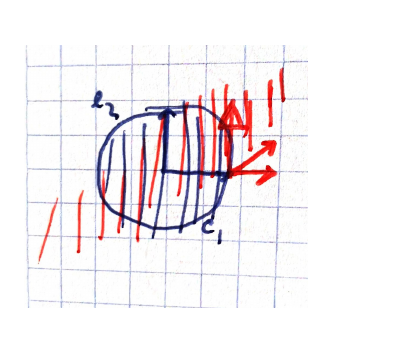
Pasted image 20231213121644.png
But what if we continue in our original basis? When we focus on a direction going out the center point, we assign a vector whose meaning is, again, the "deformation force" or "stress" that suffers the infinitesimal piece of the body around $x$ . This vector can be decomposed in two: a vector $v$ parallel to the studied direction, and other $v_{⊥}$ perpendicular to it, that tells us how we must displace the plane orthogonal to the studied direction. It looks as if you need four numbers to describe the deformation, but in the other basis you only needed two!

Here is needed that you make a mental effort to see that you have the same deformation information that giving a special basis and two scalars meaning the scale change in every direction. Because the special basis itself has to be specified (in the plane case, angle), so you actually need three numbers. And on the other hand, the lateral displacement of the orthogonal planes to every main direction must be equal, as you can understand, intuitively, in the picture below (because there is no rotation!):
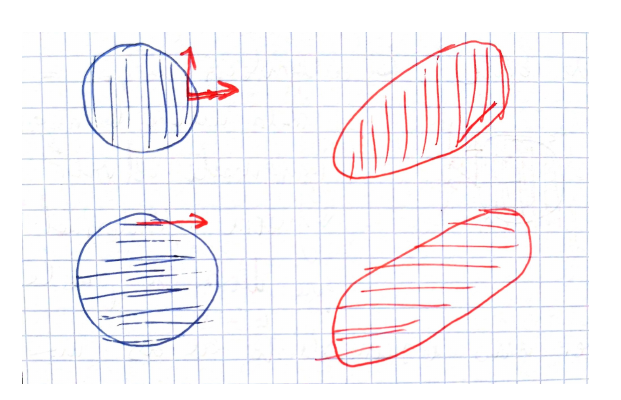
Pasted image 20231213121714.png
so you actually need tree numbers, again. This is the explanation that Cauchy tensor being symmetric.

Finally, only say that this is a very simple approach. Force and deformation are not so simply related, because it depends on the material we are using. But the important idea to get clear is that deformation is a new kind of information, not so simple like scalars and vectors. We need a tensor.