Characteristic equation of a PDE

Probably is a particular case of method of characteristics...

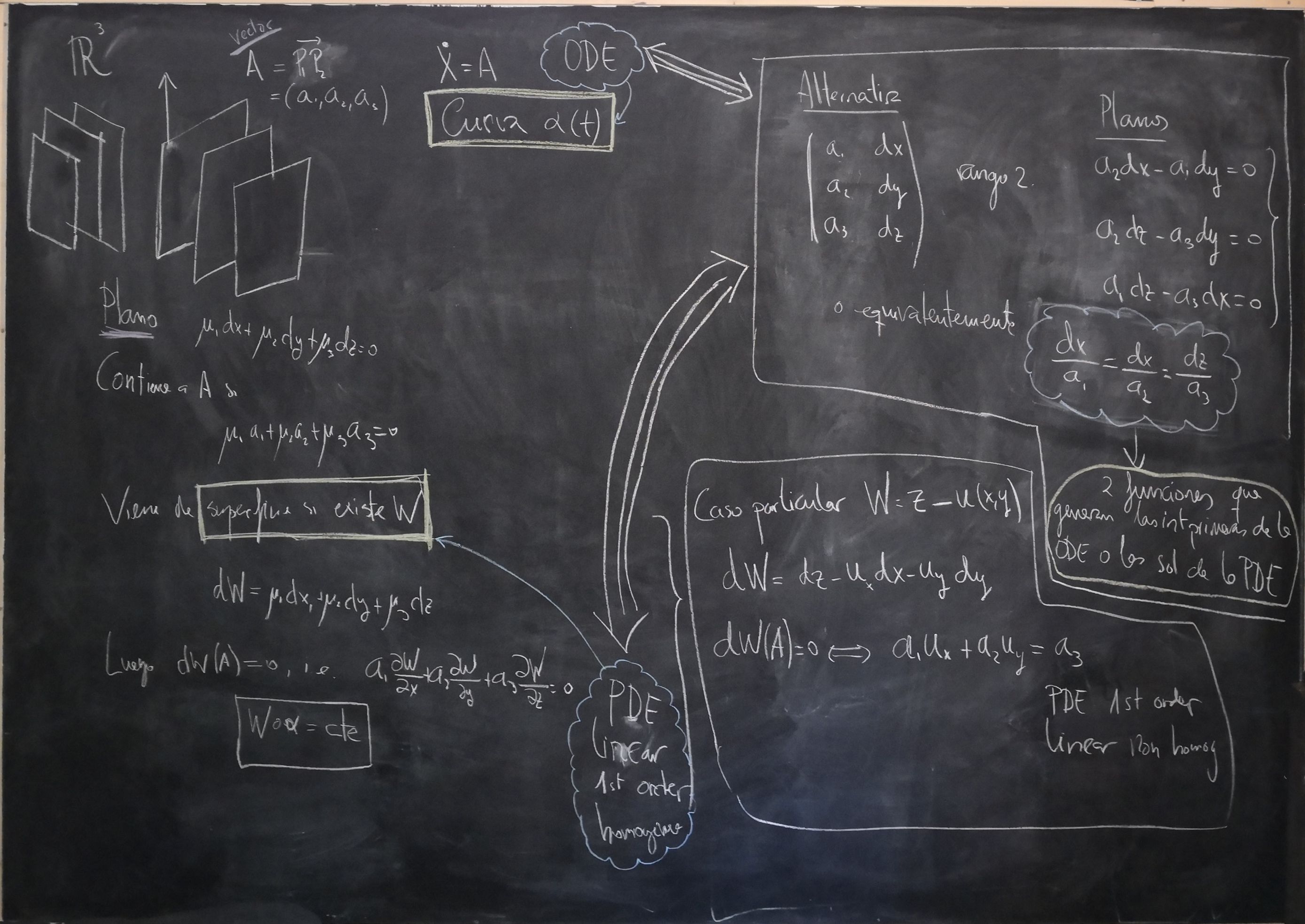
Documento 331_2.jpg

The following discussion is made for first order homogeneous linear PDEs, but according to this entry of Wikipedia it can be generalized to any first order PDE (see section Fully nonlinear case).

Given a first order homogeneous linear PDE

\begin{matrix} (1) & a_{1} \partial W / \partial x_{1} + \dots + a_{n} \partial W / \partial x_{n} = 0 \end{matrix}

where $a_{k} = a_{k} (x_{1}, \dots, x_{n})$ , we look for solutions

W : R^{n} \to R .

We can consider a solution like "surfaces" $S$ given implicitly by $W = c t e$ . Their tangent planes are given by the kernel of $d W$ .

If we define the vector field $A = a_{1} \partial x_{1} + a_{2} \partial x_{2} + \dots + a_{n} \partial x_{n}$ , a function $W$ is solution of (1) if $A (W) = 0$ , i.e., the integral curves of $A$ are contained in the surfaces $W = c t e$ .

The ODE

\begin{matrix} (2) & \dot{x} = A (x) \end{matrix}

is called the characteristic system or characteristic equation, and their integral curves are called the characteristic curves of the original PDE. Solutions of the PDE are first integrals of the characteristic equation.

The ODE (2) is, for me, like a parametric expression of a line $r$ in linear algebra (it is the case when $A (x)$ is a constant vector field). On the contrary, equation (1) is similar to an implicit expression of all the planes containing the line $r$ . The 1-form $d W$ is like an implicit equation

Method of characteristic
I think that method of characteristics is usually called to what follows.
The line $r$ above can be described by saying that it is made of vectors such that they are proportional to $(a_{1}, \dots, a_{n})$ , that is,

\frac{d x_{1}}{a_{1}} = \frac{d x_{2}}{a_{2}} = \dots

We can think of this expression as the symmetric form of a line in space ("expresión continua de la recta en el espacio" in Spanish).

From here, in the case of linear algebra, we recover several planes whose intersection gives the line $r$ :

a_{2} x_{1} - a_{1} x_{2} = 0

a_{3} x_{2} - a_{2} x_{3} = 0

. . .

In the differential context, we could recover an independent set of first integral if we were able to solve

a_{2} d x_{1} - a_{1} d x_{2} = 0

a_{3} d x_{2} - a_{2} d x_{3} = 0

. . .

The solutions are independent first integrals of the ODE or functions that generate functionally the solutions of the PDE.

In the general case, i.e. $a_{i}$ depending on too many variables, the system cannot be solved, although is useful for numerical approximation of initial or boundary value problems.

Particular case
If in the PDE we look for solutions in the form of explicit functions

W = x_{n} - f (x_{1}, \dots, x_{n - 1})

we get

a_{1} \partial W / \partial x_{1} + \dots + a_{n - 1} \partial W / \partial x_{n - 1} = a_{n}

which is the case for inhomogeneous linear PDEs.