1. First integral of a Pfaffian equation

$F$ is a first integral of the Pfaffian equation $\omega \equiv 0$ if there exists $\mu$ such that $F$ is a primitive of $\mu \omega$:

The function $\mu$ is called integrating factor.
It is said that the 1-form is a Frobenius integrable 1-form.

This terminology is taken from Maple Help page for the command FirstIntegrals:
Let $\mathcal{I}$ be a Pfaffian differential system generated by 1-forms

A real-valued function $f:M\to \mathbb{R}$ is a first integral of the Pfaffian system $\mathcal{I}$ if $df\in \mathcal{I}$. That is,

or equivalently,

Alternatively, if $\mathrm{\Delta }$ is the annihilator of $\mathcal{I}$, then $f$ is a first integral of $\mathcal{I}$ if $X(f)=0$ for all vector fields $X\in \mathrm{\Delta }$. These conditions translate into a system of homogeneous first-order linear PDEs for $f$.

There is also a purely differential-algebraic meaning to counting the number of functionally independent first integrals for $\mathcal{I}$. Let

be the derived flag of $\mathcal{I}$. Then the terminal derived system ${\mathcal{I}}_{\ell }$ (the system at which the flag stabilizes) is a Frobenius system, and the number of first integrals of $\mathcal{I}$ equals the rank of ${\mathcal{I}}_{\ell }$.

Observe that the characterization $\mathrm{df}\wedge {\theta }^1\wedge {\theta }^2\wedge \cdots \wedge {\theta }^p=0$ let us try to find the first integral without looking for the integrating factor.

2. First integral of a vector field

$F$ is a first integral of a vector field $X$ if $X(F)=0$. The meaning is that the flow of $X$ is contained in hypersurfaces $F=constant$.

Observe that a first integral of the vector field is a solution of the PDE

of which is its characteristic equation.

First integrals of a vector field are also called their invariants, and they serve to straighten the vector field: see canonical form of a regular vector field

3.a. First integral of a first order ODE system

(and therefore of a $m$th-order ODE system)

It is a first integral $F$ of the vector field $A$ associated to the system, i.e.,

Solution curves (or their prolongations, if we are in higher order) are contained in $F=constant$.

This is generalized to any system of DEs with the notion of conservation law.

3.b. First integral of an $m$th-order ODE

Given an ODE $\mathrm{\Delta }$, we call a first integral of $\mathrm{\Delta }$ to any smooth function $F$ defined on $J^m$ (the jet bundle) such that

for a never vanishing smooth function $\mu$ called integrating factor.

Equivalence with 3.a.
This definition is equivalent to the previous one, since if $A(F)=0$ then

and so

And conversely, if $D_x(F)=\mu (u_2-\varphi )$

and therefore $F_{u_1}=\mu$ and so

Relation to definition 1 above

The ODE $u_2-\varphi (x,u,u_1)$ can be though as the 1-form

In order 1, this 1-form is the only thing we have regarding the ODE, there is no more information. In higher order we have more data: the Cartan distribution. With this preliminaries we can assure:

Proposition
There exist a pair $(F,\mu )$ such that $D_x(F)=\mu \mathrm{\Delta }$ if and only if $dF=\mu \alpha$ for certain 1-form $\alpha \equiv d{u}_1-\varphi dx$ mod $\mathcal{E}$, i.e. $\alpha =d{u}_1-\varphi dx+c{\theta }_0$.
This result can be stated for any order $m$.
Proof
[xournal 126]

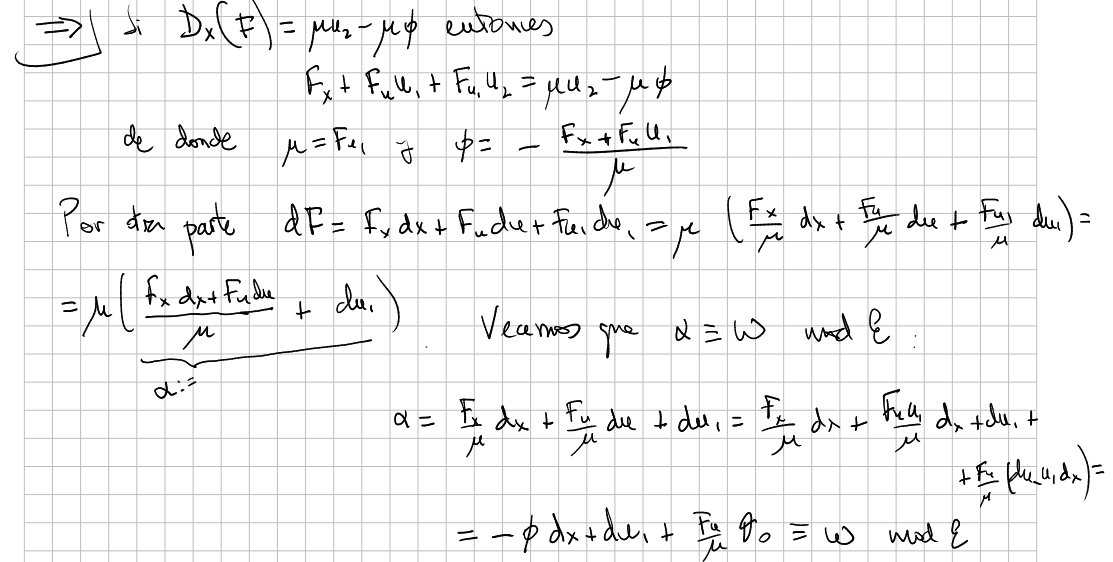
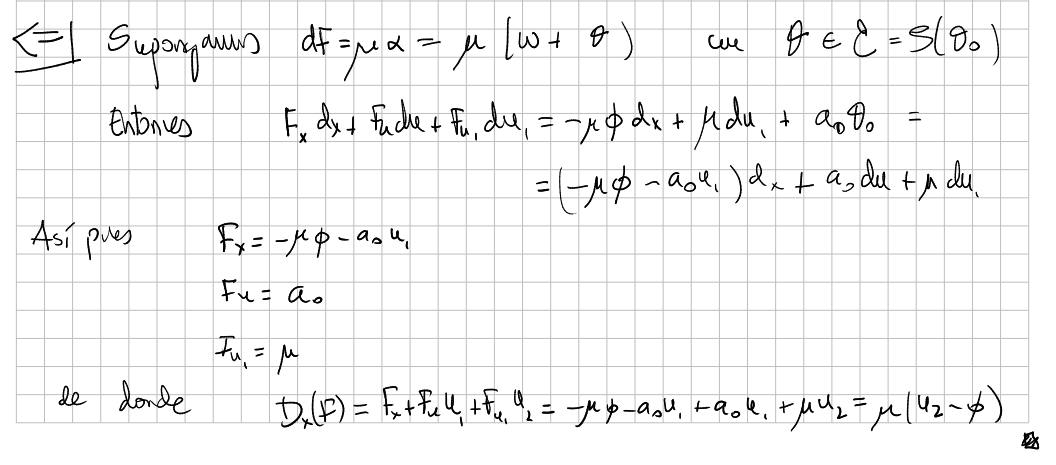
4. First integral of a distribution

Given a distribution $D$ on a manifold $M$, a function $h\in {\mathcal{C}}^{\mathrm{\infty }}(M)$ is called a first integral of $D$ if every integral submanifold of $D$ is contained in a level surface of $h$, or equivalently if $V(h)=0$ for any $V\in D$. It is coherent with this definition.