Prolongation of a diffeomorphism

Consider a diffeomorphism of the total space of a smooth vector bundle $E$

φ : E \to E

We can define a transformation $φ^{(k)} : J^{k} E \to J^{k} E$ following the same ideas as below .

Prolongation of a group action

[Olver 1986] page 98

Suppose a group $G$ acting on a the total space of a smooth vector bundle

π : E \to M

We are going to define a new action on the jet bundle.

Let $g \in G$ , $g : E \to E$ . Then we define

p r^{n} g : J^{n} (E) \to J^{n} (E)

in the following way. Consider $P = [s]_{x}^{n} \in J^{n} (E)$ and $p = π_{0} (P) = s (x) \in E$ (see here the definition of $π_{1}$ ).

Suppose we can shrink the domain of $s$ to $U \subseteq M$ in such a way that the set $g (s (U))$ is the image of another section $\tilde{s}$ (that is, $\tilde{s} (\tilde{U}) = g (s (U))$ ) and denote $\tilde{x} = π (g \cdot p)$ . Then we define

p r^{n} g (P) = [\tilde{s}]_{\tilde{x}}^{n}

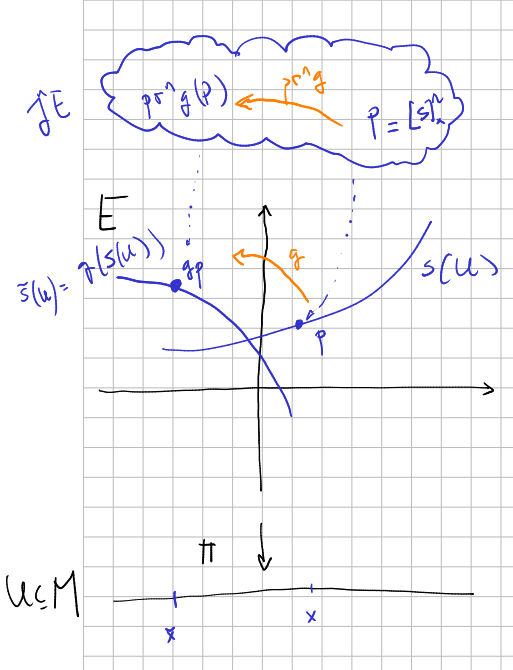
Pasted image 20211023130228.png

In coordinates

Anco_2002 page 62. I think is BETTER in xournal_041. Also in Mansfield_2010 page 32.