Energy-momentum tensor

Aka stress-energy-momentum tensor field or stress-energy tensor field. I guess it is related to Cauchy stress tensor.

Introduction

First, observe that the charge of a particle is a well-defined quantity, in the sense that it is independent of the vielbein we are using. Every particle has a well-defined charge, as confirmed by experiments (see discussions here). We can consider the evolution of lots of particles with the same charge by assuming a continuum, and this lead us to the notion of four-current: we need several numbers to characterize the evolution of the infinite charges along time.
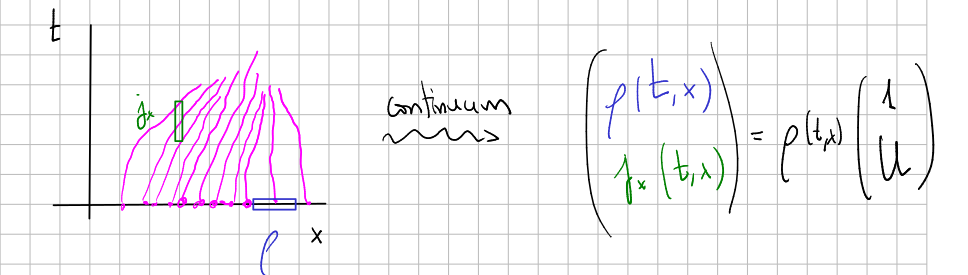
Pasted image 20241009165013.png

In the case of energy, it turns out that it is not a well-defined quantity (it changes with a Lorentz transformation), but four-momentum is. So we apply the construction given in four-current to the vector quantity $P$ .

To be continued:

see this answer
think of dust, in the video.

In General relativity

From Schuller GR.

Definition (Energy-Momentum Tensor).
Let $S_{matter} [. . ., g]$ be any matter action that couples to the metric, for example

S_{M a x w e l l} [A, g] := \frac{1}{4} \int_{M} d x^{4} \sqrt{- g} F_{a b} F_{c d} g^{a c} g^{b d} .

Then we define the components of the energy-momentum tensor as the Euler-Lagrange equations with respect to $g$ :

T^{a b} := \frac{- 2}{\sqrt{- g}} [\frac{\partial L_{matter}}{\partial g_{a b}} - \frac{\partial}{\partial x^{s}} (\frac{\partial L_{matter}}{\partial (\partial_{s} g_{a b})}) + \frac{\partial}{\partial x^{t}} \frac{\partial}{\partial x^{r}} (\frac{\partial^{2} L_{matter}}{\partial (\partial_{t} \partial_{r} g_{a b})}) - \dots],

where the terms continue with alternating signs.

Remark
In the above definition we said "that couples to the metric." This is true for all of the classical matter fields of the standard model, and so we will always have this in this course.

Remark
The minus sign in the above definition is included to ensure $T (ϵ^{0}, ϵ^{0}) > 0$ , which tells us that energy is positive.

Example
For the Maxwell action, the energy-momentum tensor is

T_{a b} = F_{a m} F_{b n} g^{m n} - \frac{1}{4} F_{m n} F^{m n} g_{a b} .

Remark
In practice, usually the energy-momentum tensor is not obtained from an action, but it is assumed regarding the phenomena been studied.