Normed space

A normed vector space is a vector space equipped with a norm. It is a particular case of a metric space.
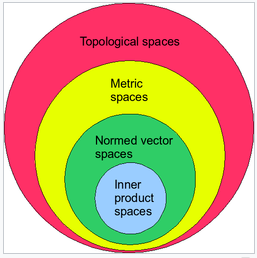
Pasted image 20211017084555.png
If it is Cauchy complete with respect to the topology induced by the norm, is a Banach space.

Examples of norms:

\begin{aligned} ∥ x ∥_{p} = {(\sum_{i = 1}^{n} {| x_{i} |}^{p})}^{1 / p}, for p \in [1, \infty) \\ ∥ x ∥_{\infty} = max_{i = 1 : n} | x_{i} | \end{aligned}

Especial class of norms: matrices norms. For example: in the matrix algebra $M_{n}$ , given a matrix $A$ we define the infinity norm

∥ A ∥_{\infty} = {max}_{i \leq i \leq n} \sum_{j = 1}^{n} | a_{i j} | .

It is induced by the infinity norm of $R^{n}$ .

Important notion operator on a normed space.