Geometric algebra

An Intuitive Introduction

For a more in-depth explanation, you can refer to "What is Geometric Algebra?" in the Calibre Library. In a nutshell, the exterior algebra can be constructed for any vector space $V$ , using $V$ itself rather than its dual $V^{*}$ . This results in a graded algebra:

Λ (V) = Λ^{0} (V) \oplus Λ^{1} (V) \oplus Λ^{2} (V) \oplus \dots \oplus Λ^{n} (V)

The elements of this algebra can be interpreted as scalars, vectors, bivectors, trivectors, etc. A bivector $u \land v$ can be understood as the plane spanned by $u, v$ along with the area of the parallelogram and the orientation from $u$ to $v$ . Similar interpretations can be made for a $k$ -vector.

In the algebra $Λ (V)$ , we have operations like addition, scalar multiplication, inner product for vectors, and wedge product for any $k$ -vectors. All of these can be generalized by a new operation known as the geometric product. For vectors, it takes the following form:

u v = u \cdot v + u \land v

Geometric Algebra in 2D and Complex Numbers

When we set $V = R^{2}$ , it can be shown that $G^{2} = Λ (R^{2})$ naturally contains complex numbers. Given a basis ${e_{1}, e_{2}}$ , we have:

\begin{aligned} e_{1} e_{1} & = 1, \\ e_{2} e_{2} & = 1, \\ e_{1} e_{2} & = - e_{2} e_{1}, \\ (e_{1} e_{2})^{2} & = - 1, \end{aligned}

Therefore, we interpret $e_{1} e_{2}$ as the imaginary unit $I$ . Furthermore, it can be shown that:

$R \oplus Λ^{2} (R^{2})$ is isomorphic to $C$ , with its usual internal rotations.
$R \oplus Λ^{2} (R^{2})$ acts on $Λ^{1} (R^{2}) = R^{2}$ as dilation-rotations. Specifically, the exponent $e^{I θ}$ , defined as $\cos (θ) + \sin (θ) I$ , rotates a vector $a \in R^{2}$ by $2 θ$ through the formula $a^{'} = e^{- I θ} a e^{I θ}$ .

Note: Although $e^{I θ}$ acts on $Λ^{1} (R^{2})$ to produce a rotation of $θ$ , which seems natural, this behavior is not generalizable to all dimensions.

Complex number has a doubled "personality": they represent vectors, on the one hand, and operations on vectors, on the other. From the Geometric Algebra viewpoint, everything is more coherent, since in $G^{2}$ we have:

The real plane $R^{2}$ itself, that is, its grade 1 members.
The even subalgebra $R \oplus G_{2}^{2}$ that operates over $R^{2}$ in the sandwiched way.

Geometric Algebra in 3D and Quaternions

When we take $V = R^{3}$ , $G^{3} = Λ (R^{3})$ contains quaternions $H$ in a natural way. With a fixed basis ${e_{1}, e_{2}, e_{3}}$ , it turns out that $e_{2} e_{3}, e_{1} e_{3}, e_{1} e_{3}$ behave like the imaginary units $i, j, k$ in $H$ . Therefore:

$Λ^{2} (R^{3})$ are the pure imaginary quaternions.
$R \oplus Λ^{2} (R^{3})$ is isomorphic to $H$ , maintaining its usual internal properties.
An unitary vector $a \in R^{3}$ defines a reflection in $R^{3}$ along the plane orthogonal to it through the formula $x^{'} = - a x a$ .
$R \oplus Λ^{2} (R^{3})$ acts on $Λ^{1} (R^{3}) = R^{3}$ as rotations. Specifically, the exponent $e^{B θ}$ rotates a vector $a \in R^{3}$ by $2 θ$ along the plane given by $B$ using the formula $e^{- B θ} a e^{B θ}$ .

Axiomatic approach

We can invert the entire construction process to define a geometric algebra as follows:
Definition:
A geometric algebra is a set $G$ equipped with two composition laws—addition and multiplication (referred to as the geometric product)—that meet the following criteria:

$G$ is a (potentially non-commutative) graded ring with a unit element. The neutral elements for addition and multiplication are denoted by 0 and 1, respectively.
The grade-0 elements, $G_{0}$ , constitute a field with characteristic 0 that includes the neutral elements 0 and 1. The elements of $G_{0}$ commute under multiplication with any element in $G$ , meaning they are contained in the center of $G$ . Hence, $G$ can be viewed as an associative algebra over $G_{0}$ .

Elements of $G_{0}$ are called scalars or 0-vectors.
$G$ includes a subset $G_{1}$ that is closed under addition, and its elements are termed 1-vectors.

The square of a 1-vector is a scalar, and if $a \neq 0$ ,
$a^{2} = | a |^{2} \neq 0$
For $a \in G_{1}$ and $A_{k} \in G_{k}$ , we can define the inner product as
$a \cdot A_{k} = \frac{1}{2} (a A_{k} - (- 1)^{k} A_{k} a)$
and the outer product as
$a \land A_{k} = \frac{1}{2} (a A_{k} + (- 1)^{k} A_{k} a)$
Consequently,
$a A_{k} = a \cdot A_{k} + a \land A_{k}$
We assume that:
- $a \cdot A_{k} \in G_{k - 1}$
- $a \land A_{k} \in G_{k + 1}$
There exists a certain $n \in N$ such that for every $A_{n} \in G_{n}$ ,

a \land A_{n} = 0

and

G_{j} \neq \emptyset

for $j = 0, 1, \dots, n$ .

Some remarks:

The neutral $0 \in G_{0}$ (as a scalar) is identical to $0 \in G_{1}$ (as a 1-vector).
The first part of axiom 3 is equivalent to: for any $u, v \in G_{1}, u \cdot v \in G_{0}$ . Thus, it can be deduced from axiom 4.
Elements of $G_{r}$ are known as $r$ -vectors. If an element contains only one term, it is called a simple $r$ -vector or $r$ -blade. In general, a geometric product of $r$ vectors (which are not necessarily orthogonal) is termed an $r$ -versor.
If $G_{1}$ has dimension 3, then one can show that the linear combination of 2-blades can always be reduced to a single 2-blade (for instance, in $R^{3}$ , two planes always share a common line). However, this does not hold in higher dimensions.
Concerning axiom 2, every ring $R$ (even a non-commutative one) can be viewed as an associative algebra over its center. Conversely, if $R$ is an associative algebra over a commutative subring $S$ , then $S$ is a subset of the center of $R$ .
Within the list of axioms, we have incompletely defined two products. Several properties can be shown about these products that one would intuitively expect, such as the associativity of the wedge product and the distributive rules for both the inner and wedge products.
The definitions of the inner and wedge products within the axioms can and should be generalized to any pair $A_{r}, B_{s}$ of multivectors:
$A_{r} \cdot B_{s} := {⟨ A_{r} B_{s} ⟩}_{| r - s |}$
and
$A_{r} \land B_{s} := {⟨ A_{r} B_{s} ⟩}_{r + s}$
where $⟨ ⟩_{j}$ signifies projection over $G_{j}$ .
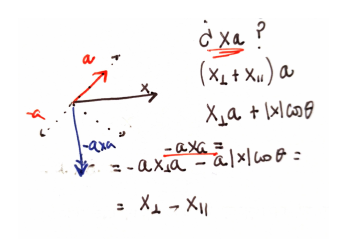
To understand the significance of $a \cdot B$ , let $B = b \land c$ . Following the definitions, we find:
$a \cdot (b \land c) = \frac{1}{4} [a b c - a c b - b c a + c b a]$
Manipulating this equation leads to:
$a \cdot (b \land c) = (a \cdot b) c - (a \cdot c) b$
This expression shows that $a \cdot (b \land c)$ is a vector contained in the plane spanned by $b$ and $c$ and is orthogonal to the projection of $a$ onto that plane.
Two vectors are orthogonal if $u \cdot v = 0$ . This implies $u v = u \land v$ , and vice versa. For three orthogonal vectors ${e_{i}}$ , $e_{i} \cdot e_{j} = 0$ implies:
$e_{1} e_{2} e_{3} = e_{1} \land e_{2} \land e_{3}$
Another useful definition is that of reversion. It is the unique operation in $G$ satisfying:
$\begin{aligned} (A B)^{†} & = B^{†} A^{†}, \\ (A + B)^{†} & = A^{†} + B^{†}, \\ ⟨ A^{†} ⟩_{0} & = ⟨ A ⟩_{0}, \\ a^{†} & = a if a = ⟨ a ⟩_{1} \end{aligned}$
This implies:
$(a_{1} a_{2} \dots a_{r})^{†} = a_{r} \dots a_{2} a_{1}$
Yet another definition is magnitude. For any multivector $A \in G$ :
$| A | = {⟨ A^{†} A ⟩}_{0}^{1 / 2}$
Finally, a rotor is defined as a geometric product of an even number of unit vectors such that $R^{- 1} = R^{†}$ .

Geometric interpretations

Two key insights (see this video):

"The geometric product contracts parallel parts and join perpendicular parts of shapes".
"The geometric product of two vectors $a$ and $b$ represents a linear transformation bringing $a$ to something proportional to $b$ ".

More specific interpretations

Given a unit vector $a$ , the transformation $x \mapsto - a x a$ is a reflection on the hyperplane orthogonal to $a$ .
Given a bivector $b \land c$ , with $c$ unitary WLOG, it can be interpreted as the geometric product of two orthogonal vectors $$
b\wedge c=bc^2\wedge c=
[(b\cdot c)c+(b\wedge c)c]\wedge c=(b_{|}+b_{\perp})\wedge c=b_{\perp}\wedge c=b_{\perp}c.

- M o r e o v e r, w e c a n f i n d $ e_{1} $ a n d $ e_{2} $ w i t h n o r m 1 a n d o r t h o g o n a l, a n d $ e_{1} $ p a r a l l e l t o $ c $ s u c h t h a t t h e r e e x i s t s $ λ \in R $ :

b\wedge c=\lambda e_1\wedge e_2.

I n f a c t, g i v e n a n y o t h e r v e c t o r $ x $ i n s i d e t h e p l a n e $ {b, c} $, y o u c a n s u p p o r t t h e b i v e c t o r o v e r $ x $ . T h a t i s, t h e r e a r e $ e_{1}^{'} $ a n d $ e_{2}^{'} $ o f n o r m 1, s u c h t h a t $ e_{1}^{'} $ i s p a r a l l e l t o $ x $ a n d $ e_{2}^{'} $ i s o r t h o g o n a l t o $ x $ a n d

b\wedge c=\lambda e_1 ' \wedge e_2 '.

W L O G, s u p p o s e $ x $ i s o f n o r m 1. T h e n $ x = c o s (θ) e_{1} + s i n (θ) e_{2} $ . S o t a k e

e_1'=x=cos(\theta)e_1+sin(\theta)e_2

a n d

e_2 '=-sin(\theta)e_1+cos(\theta)e_2

I t^{'} s t r i v i a l t o c h e c k t h a t $ e_{1} \land e_{2} = e_{1}^{'} \land e_{2}^{'} $ a n d $ e_{1}^{'} \cdot e_{2}^{'} = 0 $ . - A v e c t o r $ x $ m u l t i p l i e d b y a b i v e c t o r $ a \land b $ . F i r s t, b y t h e p r e v i o u s p o i n t, w e c a n t h i n k i n $ a \land b $ l i k e $ λ e_{1} \land e_{2} $ . N o w, w e d i s c e r n : 1. $ x $ i s l i n e a r c o m b i n a t i o n o f o f $ e_{1} $ a n d $ e_{2} $ . T h e n $ x a \land b = x λ e_{1} \land e_{2} $ i s a c o n t r a c t i o n b y a f a c t o r $ λ $ a n d 90 d e g r e e s t u r n o f $ x $ . 2. $ x $ i s o r t h o g o n a l o f t h e p l a n e g e n e r a t e d b y $ e_{1} $ a n d $ e_{2} $ . W e h a v e t h a t

x a\wedge b= x\wedge a \wedge b

a trivector. 3. So if $x$ is a sum of a parallel component and a orthogonal component, $x$ multiplied by $a\wedge b$ gives rise to a rotation of the projection of $x$ in $\{a,b\}$, and the creation of a trivector $x_{\perp}a\wedge b= x_{\perp}\wedge a \wedge b$. ## Angles and trigonometry In GA, bivectors represent 2-dimensional directions. Any simple bivector can be written as

\theta e_1e_2

w i t h $ θ \in R $ a n d $ {e_{i}} $ u n i t a r y a n d o r t h o g o n a l v e c t o r s . T h e u n i t a r y v e c t o r s s p e c i f y t h e direction i t s e l f, a n d $ θ $ i s t h e size (a n a l o g o u s t o t h e l e n g t h o f a v e c t o r, t h a t i s a 1 - d i m e n s i o n a l d i r e c t i o n) . G i v e n t w o v e c t o r s $ a $ a n d $ b $ (t h a t w e t a k e t o b e u n i t a r y, w l o g) w e s a y t h a t t h e s i m p l e b i v e c t o r $ θ e_{1} e_{2} $ is the angle formed by them i f

ab=e^{\theta e_1 e_2}

w h e r e w e t a k e a s a d e f i n i t i o n

e^A=1+A+A^2 /2+\cdots=\lim_N (1+\frac{A}{N})^N

R e a l a n a l y s i s l e t u s a s s u r e t h a t t h i s e x p r e s s i o n i s w e l l d e f i n e d w h e n $ A $ i s a 2 - b l a d e . I n f a c t, s i n c e $ e_{1} e_{2} e_{1} e_{2} = - 1 $, w e c a n w r i t e

e^{\theta e_1 e_2}=cos(\theta)+e_1 e_2sin(\theta)

w h e r e $ c o s $ a n d $ s i n $ a r e d e f i n e d b y t h e i r p o w e r s e r i e s . O b s e r v e t h a t $ b = a e^{θ e_{1} e_{2}} $ a n d t h e n

b=a(cos(\theta)+e_1 e_2sin(\theta))=a\cdot cos(\theta)+ ae_1e_2 \cdot sin(\theta)

a n d f r o m h e r e w e c o n c l u d e t h a t $ a $ i s i n t h e p l a n e g e n e r a t e d b y $ e_{1} $ a n d $ e_{2} $, s i n c e o t h e r w i s e w e w o u l d h a v e a t r i v e c t o r i n t h e r i g h t h a n d s i d e o f t h e a b o v e e q u a t i o n . O f c o u r s e, $ b $ i s a l s o i n s i d e t h e p l a n e . T h e f a c t t h a t $ a b = e^{θ e_{1} e_{2}} $ c a n b e i n t e r p r e t e d a s f o l l o w s . W e h a v e t h a t

b=a e^{\theta e_1 e_2}\cong a(1+\frac{\theta e_1 e_2}{N})^N=a+\frac{\theta}{N}a_{\perp}+\cdots

w h o s e m e a n i n g i s t h a t w e a r r i v e t o $ b $ f r o m $ a $ b y a p p l y i n g a s p e c i a l infinite process . W e n e e d s u c h a n i n f i n i t e p r o c e s s b e c a u s e w e a r e producing a circle w i t h straight lines operations.! [P a s t e d i m a g e 20240412120246. p n g] (/ i m g / u s e r / i m a g e n e s / P a s t e d O n t h e o t h e r h a n d, o b s e r v e t h a t

ab=a\cdot b+a\wedge b=

=\mu +\lambda e_1e_2

a n d i s s a t i s f i e d t h a t $ μ = c o s (θ) $ a n d $ λ = s i n (θ) $ . S i n c e $ b a a b = 1 $ w e c a n s h o w t h a t

cos^2(\theta)+sin^2(\theta)=1

I n t h i s c o n t e x t, w e c a n d e f i n e $ π $ a s t h e l o w e s t r e a l p o s i t i v e n u m b e r $ θ \in R $ s u c h t h a t

e_1 e_2=e^{\frac{\theta}{2} e_1 e_2}

N o w, n a t u r a l q u e s t i o n s a r i s e : c o u l d $ π $ b e t h e s a m e f o r e v e r y p a i r o f u n i t a r y o r t h o g o n a l v e c t o r s $ e_{1}^{'}, e_{2}^{'} $ ? M o r e o v e r, i s t h e o n l y o n e ? W e c a n d e a l w i t h t h e u n i c i t y q u e s t i o n b y m e a n s o f r e a l a n a l y s i s b y s t u d y i n g t h e p a i r o f e q u a t i o n s $ $ c o s (θ / 2) = 0

s i n (θ / 2) = 1

and we will arrive to the usual conclusions.

On the other hand, suppose $e_{1}^{'} e_{2}^{'}$ are other unitary and orthogonal vectors. Then

e^{\frac{π}{2} e_{1}^{'} e_{2}^{'}} = c o s (π / 2) + e_{1}^{'} e_{2}^{'} s i n (π / 2) = e_{1}^{'} e_{2}^{'}

So $π$ is universal for every 2-direction.

From here we can conclude usual facts like

e^{π i} = - 1

where we have called $i = e_{1} e_{2}$ to resemble the famous expression. To see it, take any unitary $v$ spanned by $e_{1}, e_{2}$ . And then, since

- v = v e_{1} e_{2} e_{1} e_{2} = v e^{\frac{π}{2} e_{1} e_{2}} e^{\frac{π}{2} e_{1} e_{2}} = v e^{π e_{1} e_{2}}

and therefore

e^{π i} = - 1

Observe that we have used that

e^{A} e^{B} = e^{A + B}

but this is true whenever $A B = B A$ .

\bigbreak

IDEA TO FOLLOW: Could be non-simple bivectors the angle between two $r$ -blades? This way, the bivector $J$ leading to the complex structure of a complexificated vector space

J = e_{1} f_{1} + e_{2} f_{2} + \dots + e_{n} f_{n} = J_{1} + J_{2} + \dots + J_{n}

is the support for angles between two prefered $n$ -blades, in the same way that for complex numbers $i = e_{1} e_{2}$ is the support for angles.

More on this: there is a formula for the total angle between subspaces

\cos θ_{A, B} = \cos θ_{1} \cos θ_{2} \dots \cos θ_{r}

and this reminds me the product of exponentials when we decompose a sum. At the same time, it reminds me the probabilty of an intersection.