Curvature of a curve

Curvature for curves is a metric concept. It needs a metric in the "ambient space". That is, is extrinsic, it depends on the embedding of the curve or the metric you assign to the underlying space. Moreover: you could have the pseudo-Riemannian manifold of dimension 1 (i.e., curves) with different curvatures when immersed in $R^{3}$ , for example. Or in other way: you could have two different curves in $R^{3}$ such that the tangent vector have the same length in every corresponding point. They could have different curvatures but when we look at them as abstract manifolds, they have the same metric tensor.

Definition
It is the quantity

κ := ⟨ N, \frac{d}{d t} T ⟩

where $T$ is the tangent vector to the curve when it is parameterized by arc-length and $N := \frac{\frac{d}{d t} T}{| | \frac{d}{d t} T | |}$ is, by definition, the unitary normal vector to the curve.
$◼$

It is related to the torsion of a curve.

On the other hand, there are two other related concepts, when the curve is inside a surface: normal and geodesic curvature of a curve.

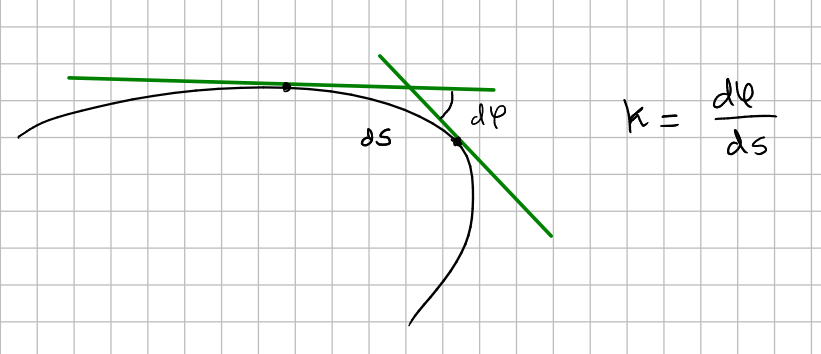
Angle variation

The curvature can be obtained in an alternative way by measuring the rate of change of the angle formed by two tangent lines:
Pasted image 20220221073519.png

Spread of the normal vector

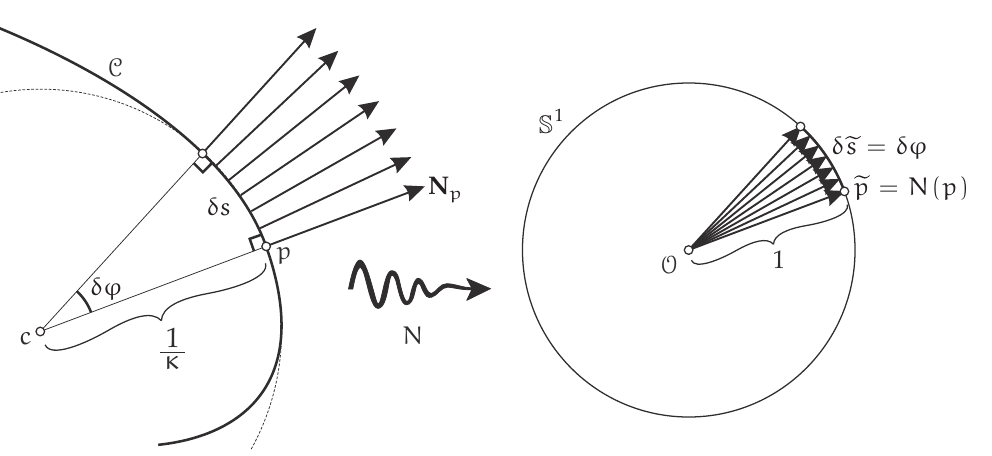
Pasted image 20220316071856.png
See @needham2021visual, page 131.
The curvature $κ$ can also be interpreted as the local length magnification factor for the map $N$ that sends every point $p$ in the curve to the tip of the normal vector $N_{p}$ translated to a fixed point $O$ . That is, in the figure:

κ = \frac{δ φ}{δ s} .

This idea leads to the idea of Gauss map for surfaces.

Formula

κ = \frac{\ddot{y} \dot{x} - \dot{y} \ddot{x}}{({\dot{x}}^{2} + {\dot{y}}^{2})^{3 / 2}}