Lie bracket

Definition

Si $X$ e $Y$ son dos campos de vectores en una variedad $M$ definimos un nuevo campo de vectores $[X, Y]$ mediante la expresión

[X, Y] (p) (f) = X (p) (Y (f)) - Y (p) (X (f)))

Hay que demostrar que es un campo.

Visualization

Lie bracket of two vector fields, $[u, v]$ , measures how is the gap when we try to draw a rectangle along flow lines of $u$ and $v$ . Let' see:
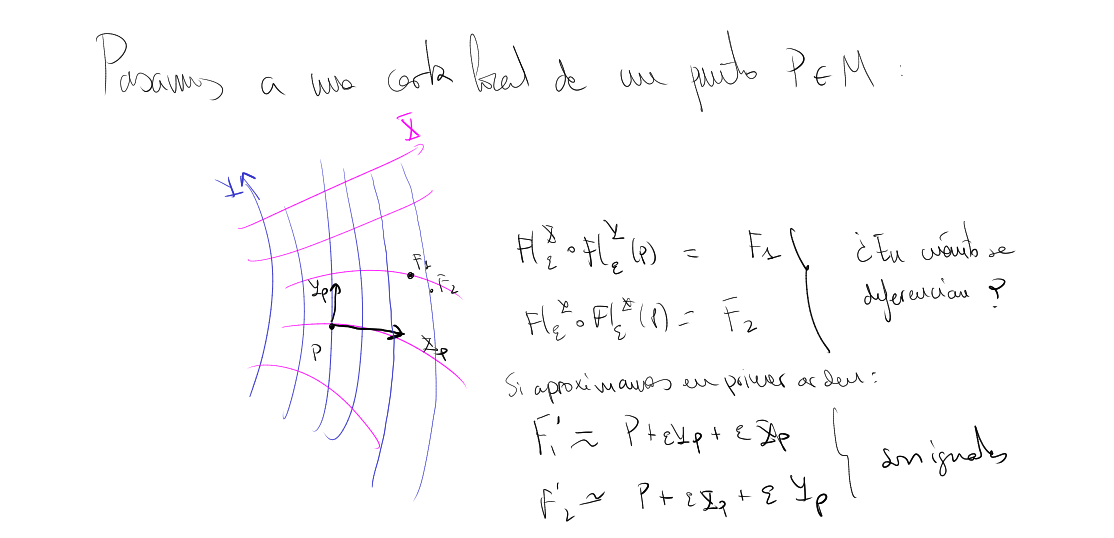
Let's go to a local chart $U$ with coordinates $x_{i}$ . If $u = u^{i} \partial x_{i}$ and $v = v^{i} \partial x_{i}$ we have that

[u, v] = (u^{j} \frac{\partial v^{i}}{\partial x_{j}} - v^{j} \frac{\partial u^{i}}{\partial x_{j}}) \partial x_{i}

On the other hand, consider a point $P$ , in the local chart. Let's call $φ$ to the flow of $v$ and $ϕ$ to the flow of $u$ . If we move a little amount $ϵ$ from $P$ following $v$ we arrive to a point $R$ that can be approximated by:

φ_{P} (ϵ) = R = P + ϵ v_{p} + O (ϵ^{2})

Let's call $R^{'} = P + ϵ v_{p}$ . Now we can move along the flow of $u$ . If we moved from $R$ we would arrive to, say, $S$ (the perfect final position), but if we begin in $R^{'}$ we will arrive to $S^{'}$ . But since we are approximating, we actually arrive to a certain $S^{″}$ in the following way:

ϕ_{R^{'}} (ϵ) = S^{'} = R^{'} + ϵ u_{R^{'}} + O (ϵ^{2})

where we take $S^{″} = R^{'} + ϵ u_{R^{'}}$
Pasted image 20220703105036.png
But observe that

S^{″} = P + ϵ v_{P} + ϵ (u_{P} + ϵ \frac{\partial u_{P}^{i}}{\partial x_{j}} v_{P}^{j} + O (ϵ^{2})) =

= P + ϵ v_{P} + ϵ u_{P} + ϵ^{2} \frac{\partial u_{P}^{i}}{\partial x_{j}} v_{P}^{j} + O (ϵ^{3})

If we begin our "whole approximated journey" from $P$ but beginning with the flow of $u$ instead, we would arrive to a certain $T^{″}$ , such that:

T^{″} = P + ϵ u_{P} + ϵ v_{P} + ϵ^{2} \frac{\partial v_{P}^{i}}{\partial x_{j}} u_{P}^{j} + O (ϵ^{3})

So the vector $T^{″} - S^{″}$ (remember we are in a local chart) is

T^{″} - S^{″} = ϵ^{2} [u, v]_{P} + O (ϵ^{3})

So $[u, v]$ measures the failure to close a parallelogram, in some sense.

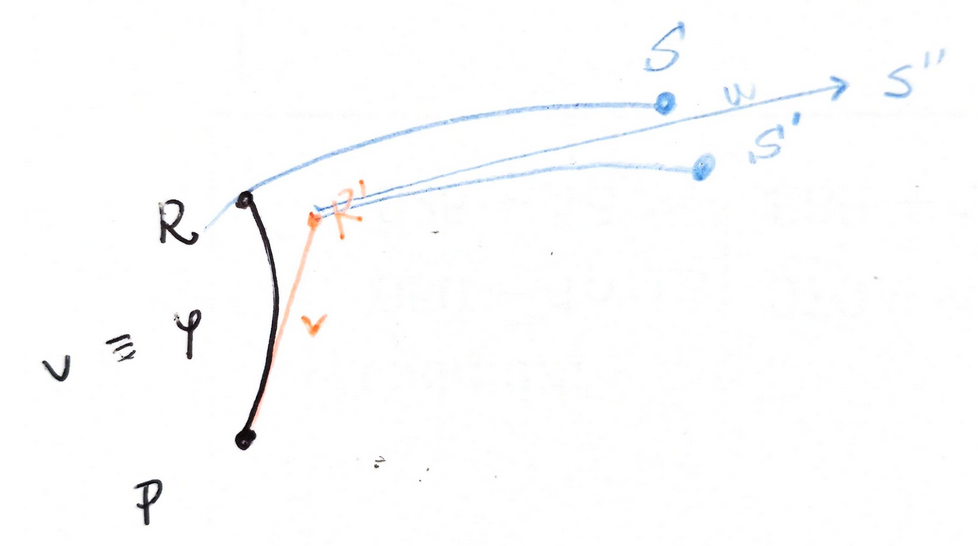
Here is a picture from TRTR, by Penrose.
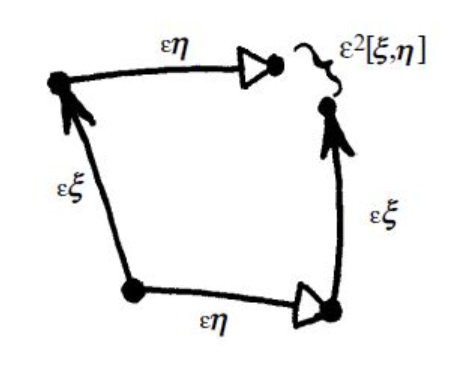
Pasted image 20220703105136.png
Related: commutativity of flows

Idea

(I think is the same as above, review and delete if needed)

To see the idea of Lie bracket, we are going to consider a local chart around a point $P$ , and to use the Taylor expansion theorem in two ways: for a curve in $R^{n}$ and for a map $R^{n} \to R^{n}$ :

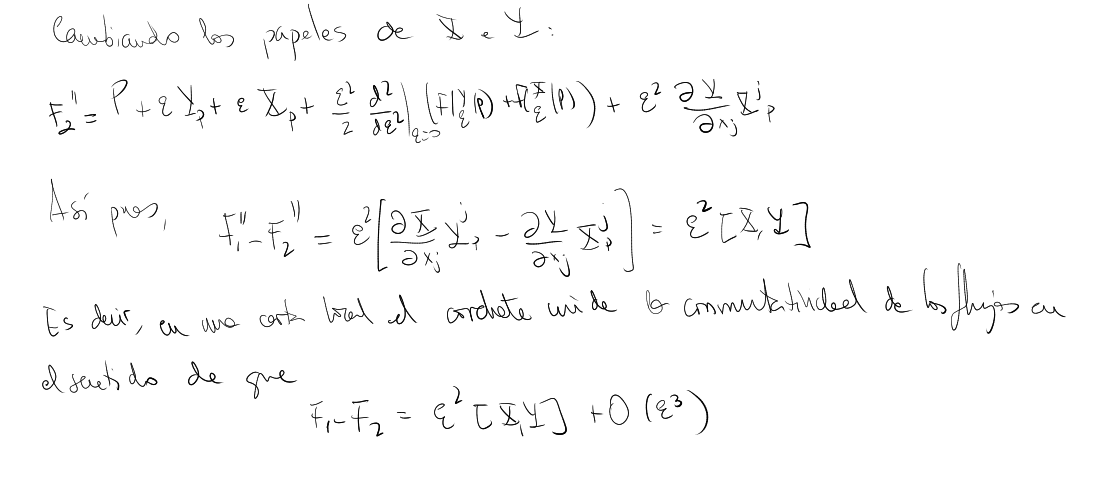
On the other hand, see TFG Adrián Ruíz for another approach of the Lie bracket as generating a zero velocity curve (lema 4.2. y lema 4.3.)

Useful formula: flow of the Lie bracket

Also we have the following formula for the Lie bracket (Wikipedia, Lie bracket of vector fields):

[X, Y]_{p} = {\frac{1}{2} \frac{d^{2}}{d t^{2}} |}_{t = 0} (Φ_{- t}^{Y} \circ Φ_{- t}^{X} \circ Φ_{t}^{Y} \circ Φ_{t}^{X}) (p) =

= {\frac{d}{d t} |}_{t = 0} (Φ_{- \sqrt{t}}^{Y} \circ Φ_{- \sqrt{t}}^{X} \circ Φ_{\sqrt{t}}^{Y} \circ Φ_{\sqrt{t}}^{X}) (p)

where we are denoting the flows of the vector fields by $Φ_{t}^{X}$ .
Proof
TFG Adrián Ruíz, teorema 4.3. $◼$

Also, from @baez1994gauge:
To make the relationship with flows precise, suppose that $v$ generates the flow $ϕ_{t}$ , and $w$ generates the flow $ψ_{t}$ . Then for any $f \in C^{\infty} (M)$ :

(v f) (p) = \frac{d}{d t} f (ϕ_{t} (p)) |_{t = 0},

and similarly

(w f) (p) = \frac{d}{d s} f (ψ_{s} (p)) |_{s = 0},

so one can check that

[v, w] (f) (p) = \frac{d^{2}}{d t d s} f (ϕ_{t} (ψ_{s} (p))) - f (ψ_{s} (ϕ_{t} (p))) |_{s = t = 0} .

Coordinates expression for the Lie bracket

If $u = u^{i} \partial x_{i}$ and $v = v^{i} \partial x_{i}$ we have that

[u, v] = (u^{j} \partial_{x_{j}} v^{i} - v^{j} \partial_{x_{j}} u^{i}) \partial x_{i}

Other remarks

It can be shown that is the same as Lie derivative of vector fields.
It is bilinear, and also satisfies
- Alternativity: $[x, x] = 0$
- Jacobi identity: $[x, [y, z]] = [[x, y], z] + [y, [x, z]$
If we abstract the properties of the Lie bracket we arrive to the notion of Lie algebras.
See also relation of Lie derivative, covariant derivative and torsion.
Lie bracket has to do with Clairaut's theorem: $[\partial_{x_{i}}, \partial_{x_{j}}] = 0$ .
It implies the commutativity of flows.