Riemannian metric (or pseudo-Riemannian)

Definition
(@sharpe2000differential page 238)
A pseudo-Riemannian metric on a smooth manifold $M$ is a smooth function $q_M:TM\to \mathbb{R}$ whose restrictions $q_x:T_{x}M\to \mathbb{R}$ are all non-degenerate quadratic forms.
The metric is called Riemannian if the associated bilinear forms are positive definite.
$◼$

Another definition:
Equivalently, following notation in \cite{malament}, we can say that a (pseudo-Riemannian) metric is a smooth field $g_{ab}$ on $M$ that is symmetric and invertible, i.e., there exists other smooth field $g^{ab}$ on $M$ such that $g_{ab}{g}^{bc}={\delta }_a^c$.

It is usually called pseudo-Riemannian or pseudo-metric if is not definite positive.

In the note dual vector space can be seen how to construct the inverse. It requires the non-degenerate condition of the metric. In fact is equivalent.

The inverse field is also symmetric:

We can watch it in diagrammatic notation:

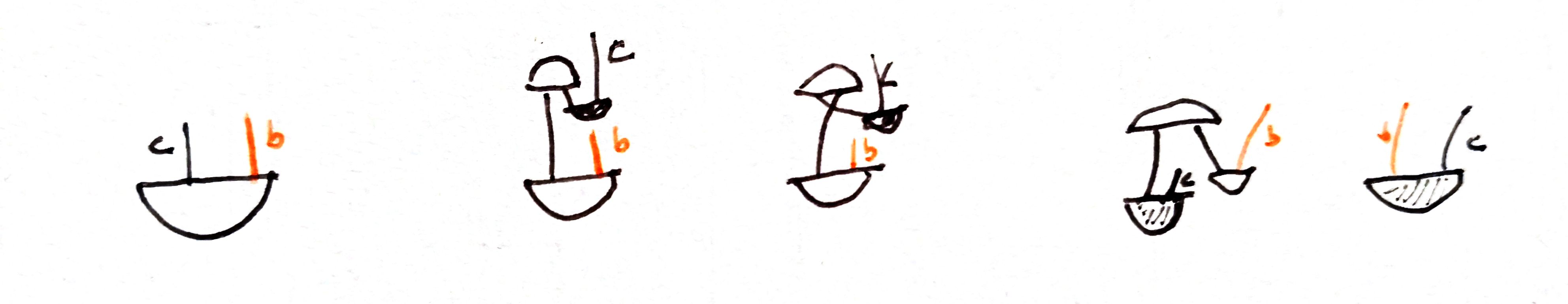
It has associated a particular vector bundle connection in $TM$, (i.e., a linear connection) the Levi-Civita connection. See relationship parallel transport, covariant derivatives and metrics.

Every manifold can be equipped with a Riemannian metric.

(This is related to the extension and reduction of a principal bundle)

We can endow $M$ with a Riemannian metric as follows: Let $\{(U_{\alpha },{\phi }_{\alpha })\}$ be an open cover of $M$ which trivializes $TM$. On each $U_{\alpha }$, choose a frame for $TM{|}_{U_{\alpha }}$ and declare it to be orthonormal (a basis on a vector space determines a metric, see dual vector space#No natural isomorphism). Let $g_{\alpha }$ denote this inner product on $TM{|}_{U_{\alpha }}$. Now use a partition of unity ${\rho }_{\alpha }$ to splice them together, i.e. define

This is clearly symmetric; $g(u,u)\ge 0$; and $g(u,u)=0$ iff $u=0$. Furthermore, it is smooth, and so defines a Riemannian metric on $M$.

Interestingly, not every manifold admits a pseudo-Riemannian metric, see this MSE question.