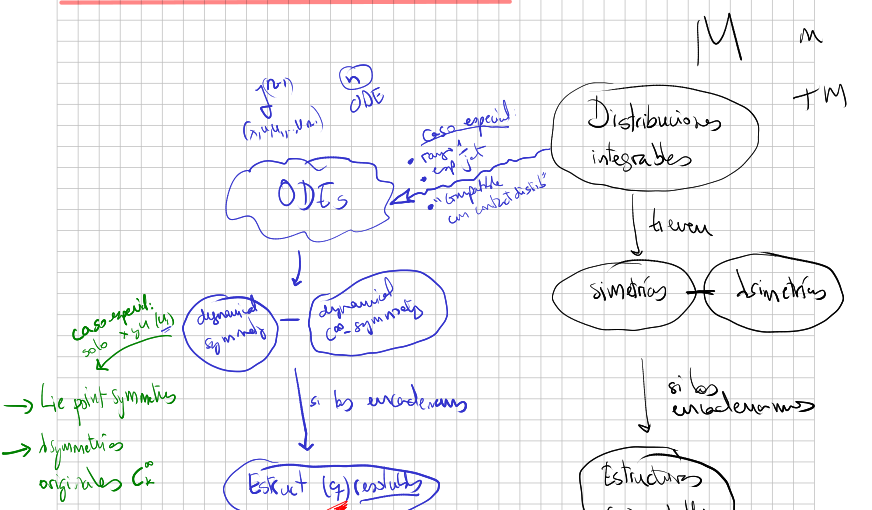
Symmetry of a distribution

A symmetry of a distribution $D$ is a diffeomorphism $ϕ : M \to M$ such that preserves $D$ , i.e., $ϕ_{*} (D) = D$ .
It can be shown (exercise 3.10 in [Vitagliano 2017]) that:

symmetries map locally maximal integral manifolds to locally maximal integral manifolds.
a diffeomorphism $ϕ$ is a symmetry if and only if for every $ω$ annihilating all $X \in Γ (D)$ , $ϕ^{*} (ω)$ annihilates all $X \in Γ (D)$ .

Infinitesimal symmetries

An infinitesimal symmetry is a vector field $X$ such that its flow is made of symmetries. They are denoted by $Sym (D)$ .
By abuse of language they are also called "symmetries". It can be shown (exercise 3.11 [Vitagliano 2017] or [Lychagin 1991] theorem 1) that they can be characterized in two other ways:

Suppose $Z$ is a distribution:

A nowhere-vanishing vector field $X$ on $M$ is called a symmetry of an involutive distribution $Z = S ({Z_{1}, \dots, Z_{r}})$ if :
1. ${Z_{1}, \dots, Z_{r}, X}$ is independent for every $p \in M$ ,
2. there exist smooth functions $c_{i}^{k}$ ( $i, k = 1, \dots, r$ ) such that

[X, Z_{i}] = \sum_{k = 1}^{r} c_{i}^{k} Z_{k}, i = 1, \dots, r .

They can be also characterized from the point of view of the dual description of the distribution: for every $ω \in Z^{*}$

L_{X} (ω) \in Z^{*} .

In this case the vector field $X$ is a symmetry of a Pfaffian system.

On the other hand, infinitesimal symmetries constitute a Lie subalgebra of the vector fields of the manifold (exercise 3.11 [Vitagliano 2017]).

Transitive symmetry algebra

(see [Doubrov 2016] page 42)
A Lie subalgebra $g \subseteq Sym (D)$ is called a transitive symmetry algebra of $D$ if

g + D_{p} = T_{p} M

being $g (p) = {X_{p} \in T_{p} M : X \in g} .$
Also, it is called a simply transitive symmetry algebra if additionally for any $X \in g$ it is satisfied that $X_{p} \in D_{p}$ if and only if $X \in Γ (D)$ .

Given any Lie subalgebra $g \subseteq Sym (D)$ , the associated local group of transformations $G$ maps integral submanifolds into integral submanifolds (see above). If we call $M$ to the set of integral submanifolds, the Lie algebra is transitive if and only if the action of $G$ on $M$ is locally transitive.

Characteristic symmetries

A characteristic symmetry (also called trivial symmetry) is an infinitesimal symmetry $X$ which is inside $D$ , i.e., $X \in Γ (D)$ . They are denoted by $Char (D) \subseteq Γ (D)$ .

If every $X \in Γ (D)$ is a characteristic symmetry, we have an involutive distribution. If none of them is a characteristic symmetry then we have a completely non-integrable distribution.

The characteristic symmetries form an ideal of the Lie algebra of infinitesimal symmetries.

They correspond to the Cauchy characteristic vector fields of the Pfaffian system associated to the distribution.

Shuffling symmetries

[Lychagin 1991]
Elements of the quotient algebra

Shuf (D) = \frac{Sym (D)}{Char (D)}

are called shuffling symmetries. The flows of two different representative of a class shuffle the set of maximal integral manifolds of $P$ in the same way.

We have a natural mapping for every $x \in M$

π_{x} : Shuf (D) \to T_{x} M / D_{x}

A related idea is that of a transversal algebra of symmetries.

More ideas

Por otra parte, las symmetry of a distribution se pueden generalizar a cinf-symmetry of distribution.

Al aplicar este concepto a la distribución asociada a una ODE tenemos la noción de generalized symmetry of an ODE.

Si "encadenamos" varias aparecen las solvable structure para la distribución $Z$ .

ESQUEMA GENERAL (xournal 095)
Pasted image 20210914161521.png