Theorema Egregium

Generalization: Gauss' Equation.
Theorem
If $f:S_1\to S_2$ is a local isometry, then the Gaussian curvature of $S_1$
at $P$ equals the Gauss curvature of $S_2$ at $f(P)$.
$◼$

As a precursor of this theorem, Gauss stated 10 years before the "beautiful theorem":
If a curved surface on which a figure is fixed takes different shapes in space, then the surface area of the spherical image of the figure is always the same.

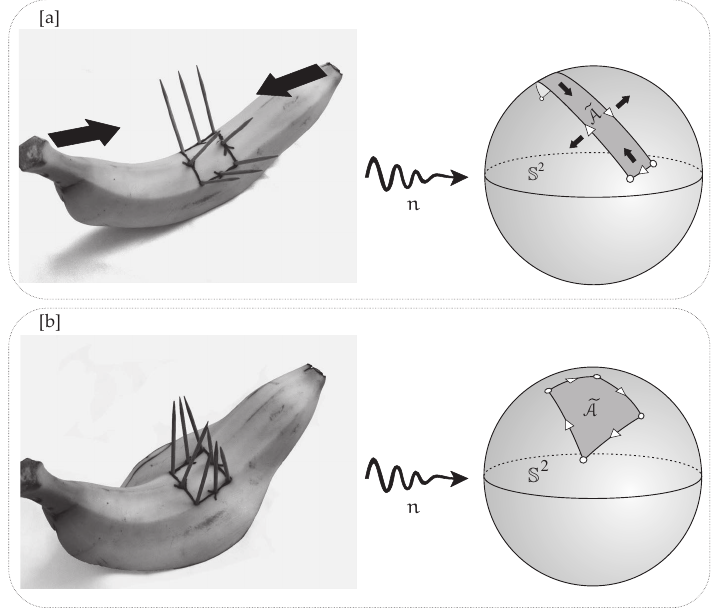
See @needham2021visual page 139

Taking into account the definition of Gauss curvature given here, it is clear that Theorema Egregium is a local version of the beautiful theorem, since $K\cong \frac{\delta \tilde{A}}{\delta A}$ and $\delta A$ is trivially invariant under isometries.

Paper folding

Among other things, this theorem shows us why paper only folds into straight lines (@needham2021visual page 221 exercise 11). The paper, at first, is flat so $K={\kappa }_1{\kappa }_2=0$. After folding it must conserve the Gaussian curvature . But if the fold were not a straight line, by inspecting the normal curvatures at a point of the fold we would conclude they are always greater than 0, which would be imposible.

Generalization

See Gauss' Equation.