Transverse geometry of a foliation
([Molino 1988], página 33)
Consiste en estudiar la geometría del espacio de hojas de una foliation dada. Este espacio topológico no siempre es una manifold (ver ejemplo [Molino 1988, página 15])
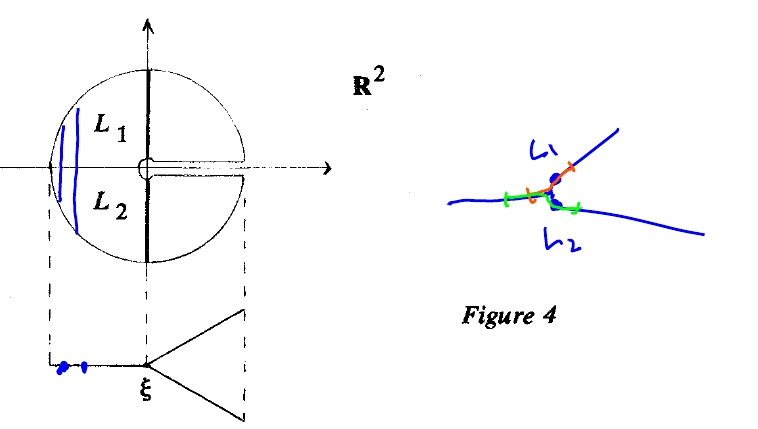
y creo que tampoco es siempre un orbifold porque las hojas no tienen por qué ser las órbitas de un grupo.
No obstante, se pueden generalizar nociones propias de las manifold, dando lugar a basic functions, transverse fields, basic differential forms, foliated principal bundles and projectable connections; que son la contrapartida de los conceptos típicos de differentiable functions, vector fields, diferential forms, principal bundles and infinitesimal connections.