Weingarten map

(Generalization to hypersurfaces: Gauss' Equation#For hypersurfaces.)
(Better explanation in second fundamental form#Generalization to surfaces in 3-dimensional manifolds via moving frames.)

For immersed surfaces in R3

It is the differential of the Gauss map $N$ :

p \in S ⟼ {d N_{p} : T_{p} S \to T_{N (p)} S^{2}}

For every $p$ , $d N_{p}$ transforms a little circle in $T_{p} S$ in an ellipse in $T_{N (p)} S^{2}$ , and is an useful way to measure extrinsic curvature. Indeed, since $d N_{p} (X)$ measures how it changes $N (p)$ in the direction $X$ (think of $d N_{p} (X) = \frac{d}{d t} (N \circ α_{X} (t))$ ) and $N (p)$ has constant module equals to 1, it turns out that $d N_{p} (X)$ is orthogonal to $N_{p}$ itself, so $d N_{p} (X) \in T_{f (p)} f (S)$ . So we can think about the Weingarten map as

d N_{p} : T_{p} S \to T_{f (p)} f (S)

It let us to speak about principal directions and principal curvatures (see the picture below obtained from a Youtube video):
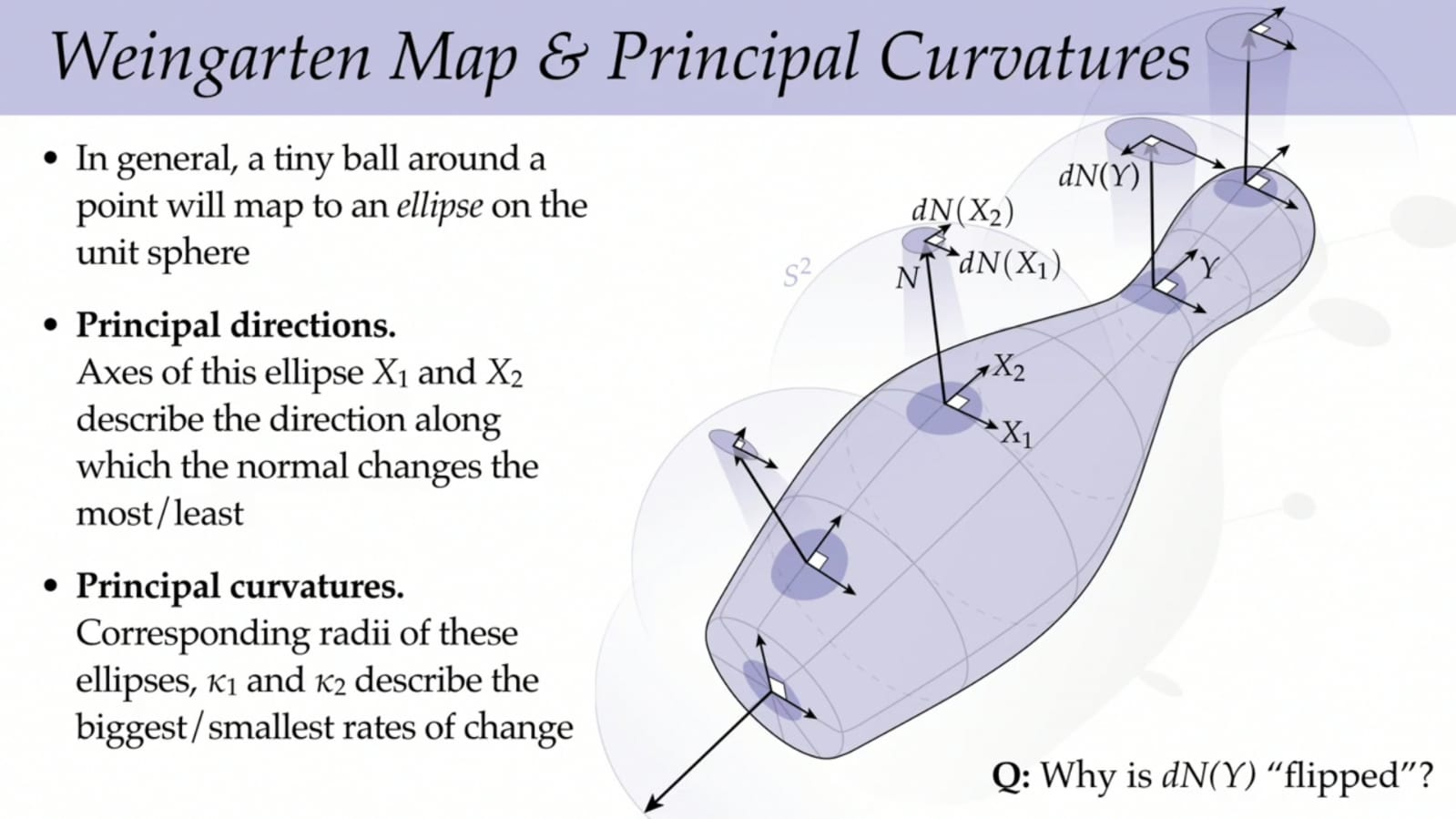
Pasted image 20211005072900.png

From the Gauss map we can define the normal curvature of an immersed surface.

The Weingarten map is related to the shape operator.