Global Gauss-Bonnet theorem

It is the global version of local Gauss-Bonnet theorem.

Theorem
Given a closed orientable surface (I think it should be immersed in ${\mathbb{R}}^3$) $S$ of genus $g$, the total curvature

where $K$ is the Gaussian curvature, satisfies

The quantity

is the Euler characteristic.
$◼$

It means that given any closed orientable surface, if we deform it in the way we like (even stretching and twisting), if we get an increase in Gaussian curvature in a point, the curvature must be decreasing in other points in order to compensate the total curvature.

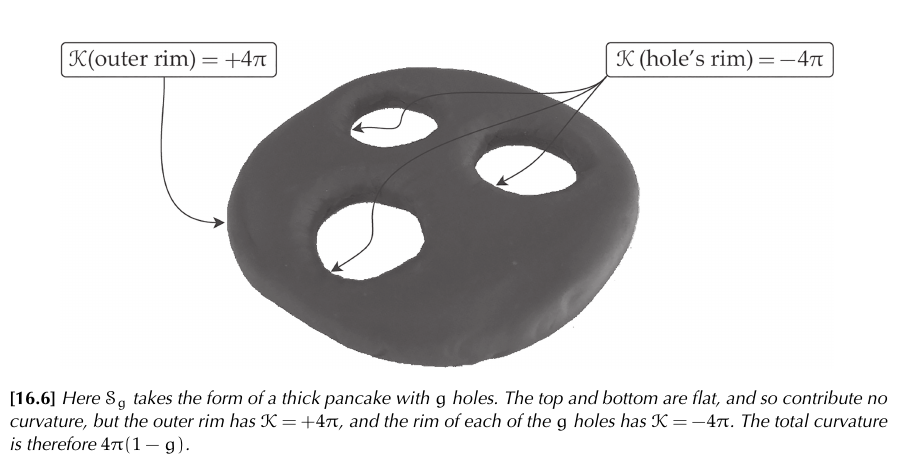
Visual idea:
(@needham2021visual pages 169-172)
In a sphere, or in any other topologically equivalent surface, the total curvature is $4\pi$, since the unitary normal vector fill ${\mathbb{S}}^2$ exactly once.
In a torus is 0, since the external side of the torus counts for $4\pi$ but the internal one add $-4\pi$, since the Gauss map reverse orientation in these points.
In the general case of a compact surface: