Inverse Scattering Method

See @Aktosun_2009. And also INVERSE SCATTERING TRANSFORM, KdV, AND SOLITONS by Aktosun, too.
The inverse-scattering method is different in the details for different equations. Hence there is no such thing as “the” inverse-scattering method.
The inverse scattering transform (IST) is a powerful mathematical technique used primarily to solve certain nonlinear partial differential equations (PDEs). It is closely related to the Fourier transform, but it generalizes the concept to handle nonlinear problems.
Here it is an scheme of how it works:
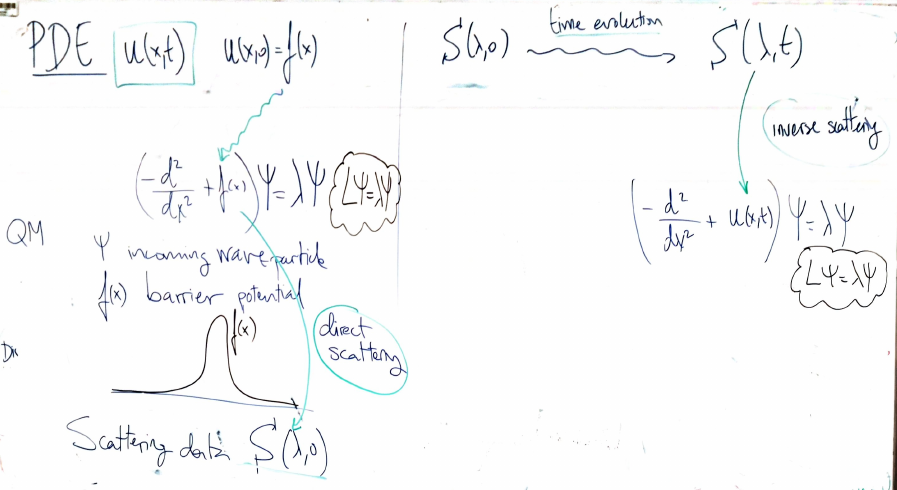
Pasted image 20230805160921.png
Given a PDE with initial condition $u (x, 0) = f (x)$ we can imagine a wave-particle propagating in a medium with some inhomogeneity or potential $f (x)$ . As the wave encounters this potential, it gets scattered. The scattering data $S (λ, 0)$ , which consists of reflection and transmission coefficients, describes how the wave is affected by the potential.
We can study how the scattering data evolves along time, obtaining $S (λ, t)$ , and from here recover $u (x, t)$ be means of an inverse scattering.

1. Direct Scattering Transform (DST)

Given a potential (or inhomogeneity) and an incident wave, the DST produces the scattering data (reflection and transmission coefficients).
For a particle in a potential $f (x)$ , the time-independent Schrodinger equation is:

\hat{H} ψ (x) = E ψ (x)

where $\hat{H}$ is the Hamiltonian operator:

\hat{H} = - \frac{ℏ^{2}}{2 m} \frac{d^{2}}{d x^{2}} + f (x)

We can interpret $ψ$ as stationary states of a special kind: that ones showing the idea of an incoming wave from the left with a reflection part and a transmitted part. I.e., for $x \to - \infty$ , we can consider:

ψ (x) \approx e^{i k x} + r e^{- i k x}

where:

The first term represents an incoming wave.
The second term represents a reflected wave with reflection amplitude $r$ .

For $x \to \infty$ , we have:

ψ (x) \approx t e^{i k x}

This represents the transmitted wave with transmission amplitude $t$ .

The probability of reflection, $R$ , is given by $| r |^{2}$ , and the probability of transmission, $T$ , is given by $| t |^{2}$ . Since the particle must be either reflected or transmitted, we have:

R + T = 1

⟹ | r |^{2} + | t |^{2} = 1

To find $r$ and $t$ , one needs to solve the Schrödinger equation within the region of the potential $u (x)$ and match the solutions at the boundaries of this region with the asymptotic solutions. This generally requires integration and might be more challenging for some potential shapes than others. Interesting example is the scattering of a Dirac delta barrier (see Griffiths Introduction to QM page 90).

Usually this problem is solved using something called Jost solutions.

2. Time evolution of the scattering data

It is performed by means of the time evolution of the Jost solutions.

3. Inverse Scattering Transform (IST)

Given the scattering data, the IST reconstructs the potential. This is a more challenging problem, analogous to reconstructing an object's shape just by looking at its shadow.