Jacobi equation

Also known as geodesic deviation equation, it relates geodesics and Gaussian curvature.
This equation describes how the separation between geodesics (as measured by a Jacobi field) evolves as we move along the geodesics.
The equation is

with the notation given here. $R$ is the Riemann curvature tensor.

In surfaces

In a 2-dimensional Riemannian manifold, the Riemann curvature tensor simplifies significantly. In particular, it can be expressed entirely in terms of the Gaussian curvature $K$. The Riemann curvature tensor in 2 dimensions is given by:

where $X,Y,Z$ are vector fields on the manifold, $g$ is the metric tensor, and $K$ is the Gaussian curvature.
So substituting this in the Jacobi equation we obtain

If the geodesic has a unitary tangent vector the equation simplifies to:

Intuitive approach of Needham

Case $n=2$

In a surface

being $\xi (t)$ the "separation" of two geodesics (@needham2021visual page 269; and proof in 274)

Proof
It uses geodesic polar coordinates. Also uses Gauss lemma.
By the way, it let us to show Minding's theorem.
$◼$
Formal statement is based on the notion of Jacobi field.

Case $n>2$

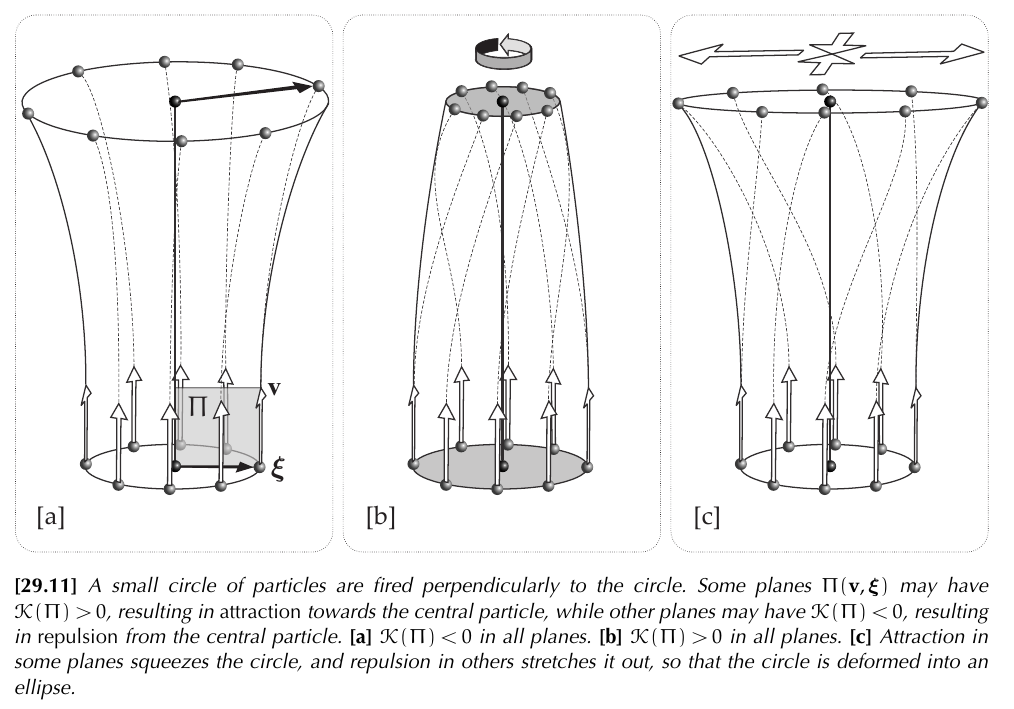
According to @needham2021visual there are two versions:

• Sectional Jacobi equation

where $\mathrm{\Pi }$ is a plane containing the tangent vector $v$ to the geodesic, $\mathcal{P}$ is the projection over this plane and $\mathcal{K}(\mathrm{\Pi })$ is the sectional curvature.

• General Jacobi equation or Equation of Geodesic Deviation

When $\mathcal{R}(\mathit{\xi },\mathbf{v})\mathbf{v}$ is not contained in $\mathrm{\Pi }$ it happens the rotation of picture b) above.