Laplace transform

Given a complex-valued function $f (t)$ with $t \in R$ , the Laplace transform is a function $F : C \to C$ such that every $F (s)$ represents the weight of the function $e^{s t}$ in the decomposition

f (t) = \frac{1}{2 π i} (\dots + F (c + 0.1 i) e^{(c + 0.1 i) t} + F (c + 0.2 i) e^{(c + 0.2 i) t} +

+ F (s) e^{s t} + \dots) =

= \frac{1}{2 π i} lim_{T \to \infty} \int_{c - i T}^{c + i T} e^{s t} F (s) d s

for any $c \in R$
In this video it is pictured like this:
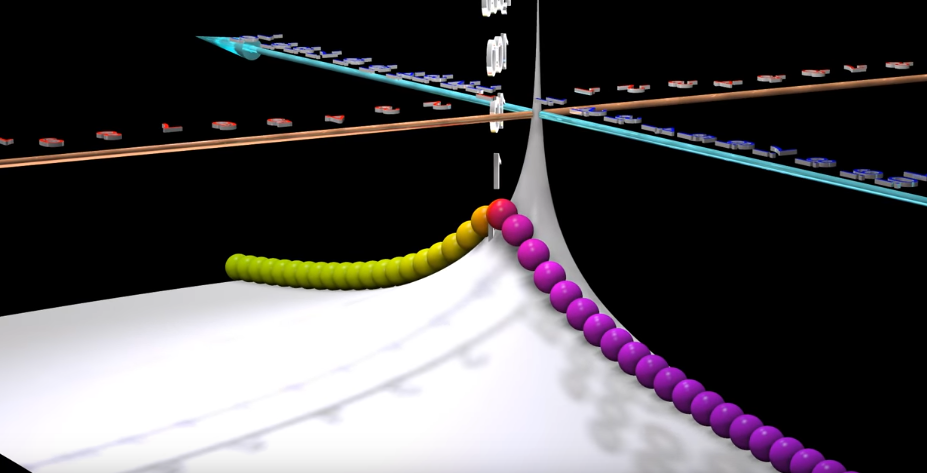
Pasted image 20220119170021.png

A particular case would be the Fourier transform, whose picture corresponds to the case $c = 0$
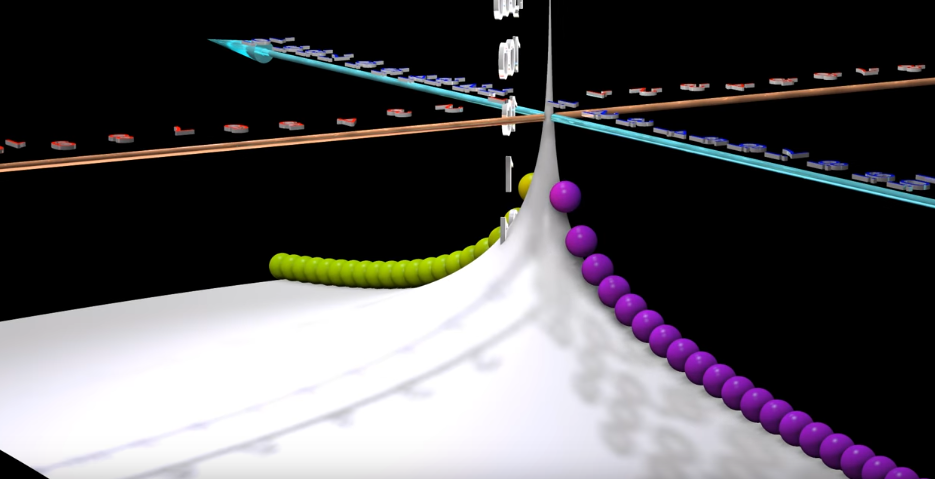
Pasted image 20220119170159.png

Both transformations has to do with the fact that some spaces of functions are Hilbert spaces, so we have a "basis". The original function can be thought as expressed in the Dirac delta basis, and the Fourier transform and Laplace transform are nothing but the expression of the same function in a different basis.

What basis?, the natural for the generator of the translation and momentum operators.

Related: Mellin transform.