Length of a curve

In a pseudo-Riemannian manifold $(M, g)$ we define the length of a curve $c : [0, 1] \to M$ by

l (c) := \int_{0}^{1} \sqrt{g (c^{'} (t), c^{'} (t))} d t

Interpretation

Length of a curve emerge from the following point of view.
Remember the definition, roughly speaking, of the Riemann integral:

\int_{a}^{b} f (x) d x = lim_{n} \sum_{i} f (x_{i}) \cdot (x_{i + 1} - x_{i})

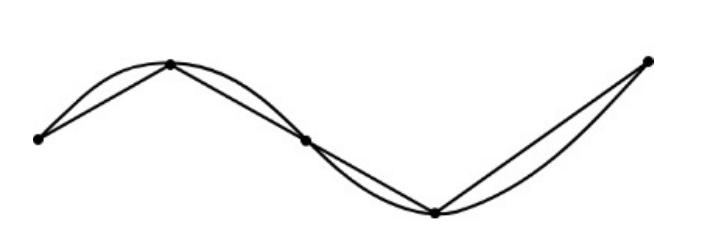
Pasted image 20240909172711.png

Now, if you want to calculate the length of a curve, you can cut it in little pieces. Suppose the curve is

γ : [a, b] \mapsto R^{n}

Then, the length is, more or less,

L = \sum_{i} g (γ (t_{i + 1}) - γ (t_{i}), γ (t_{i + 1}) - γ (t_{i}))^{1 / 2}

where $g$ is the metric of the space (the usual inner product of $R^{n}$ , for example).

But since $γ (t_{i + 1}) - γ (t_{i}) ≅ γ^{'} (t_{i}) \cdot (t_{i + 1} - t_{i})$ , if we take limit, we have

L = lim_{n} \sum_{i} g (γ (t_{i + 1}) - γ (t_{i}), γ (t_{i + 1}) - γ (t_{i}))^{1 / 2} = lim_{n} \sum_{i} g (γ^{'} (t_{i}) \cdot (t_{i + 1} - t_{i}), γ^{'} (t_{i}) \cdot (t_{i + 1} - t_{i}))^{1 / 2} =

= lim_{n} \sum_{i} g (γ^{'} (t_{i}), γ^{'} (t_{i}))^{1 / 2} \cdot (t_{i + 1} - t_{i})

But this is, by definition

\int_{a}^{b} g (γ^{'} (t), γ^{'} (t))^{1 / 2} d t

For a curve immersed in a general manifold we take local coordinates, and translate to the $R^{n}$ case.