Projections

Given a vector space $V$ , a projection is a map

P : V ⟼ V

such that $P^{2} = P$ .
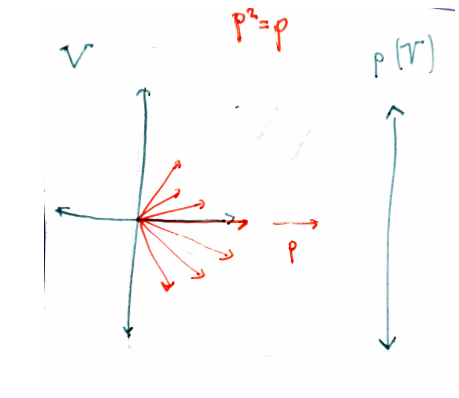
Pasted image 20211017184359.png
Informally speaking, for a projection you not only need to specify the "target" subspace, but also a "direction" along which to project (the red vectors in the picture above). So, in some sense, a projection gives us a decomposition of the vector space $V$ in horizontal and vertical subspace.

In finite dimensional vector spaces $V$ , the subspaces $U = I m (P)$ and $W = K e r (P)$ satisfies:

$P |_{U}$ is the identity operator.
$V = U \oplus W$ . Every $x \in V$ can be decomposed

x = P x \oplus (x - P x)

Other properties, valid even for infinite dimension:

The only eigenvalues allowed for a projection are $0$ and 1, even in complex vector spaces.
The product of two projection is not, in general, another projection. But it is true when they commute.
Even more generally, projections are maps that have a right inverse: $P \circ f = i d_{i m (P)}$

When we work in a Hilbert space $H$ instead of in a plain vector space $V$ , we can say that $P$ is an orthogonal projection if

⟨ P x, y ⟩ = ⟨ x, P y ⟩

that is, is a self adjoint operator.
They satisfy the following properties:

Being orthogonal is equivalent to the fact that the image $U$ and the kernel $W$ are orthogonal subspaces: let $u \in U$ and $w \in W$ then $u = P u^{'}$ and $P w = 0$ so

⟨ u, w ⟩ = ⟨ P u^{'}, w ⟩ = ⟨ u^{'}, P w ⟩

Reciprocally, any projection $P$ such that $U$ and $W$ are orthogonal satisfies, assuming $x = u_{1} + w_{1}$ and $y = u_{2} + w_{2}$

⟨ P x, y ⟩ = ⟨ P (u_{1} + w_{1}), u_{2} + w_{2} ⟩ = ⟨ u_{1}, u_{2} ⟩

and

⟨ x, P y ⟩ = ⟨ u_{1} + w_{1}, P (u_{2} + w_{2}) ⟩ = ⟨ u_{1}, u_{2} ⟩

and therefore $P$ is self-adjoint.

Given any closed subspace $U$ of $H$ it there exist an orthogonal projection $P$ such that $i m (P) = U$ . The proof (wikipedia) goes through taking the infimum of the distance...
If $P$ is an orthogonal projection, $I - P$ is an orthogonal projection and

i m (I - P) = K e r (P)

Proof:
First,

(I - P)^{2} = I^{2} - 2 P + P^{2} = I - P

And secondly, $x \in H$ , $(I - P) (x) \in K e r (P)$ since

P (I - P) (x) = P x - P x = 0

$◼$

Orthogonal projections are bounded operators. From Cauchy-Swarth

∥ P v ∥^{2} = ⟨ P v, P v ⟩ = ⟨ P v, v ⟩ \leq ∥ P v ∥ \cdot ∥ v ∥

and so

∥ P v ∥ \leq ∥ v ∥

This is similar, in some sense, to saying that is continue.

Suppose $U = i m (P)$ has dimension 1, and we take a length 1 vector $u \in U$ . If we fix an orthogonal basis we can express

P = u \cdot u^{*}

P = | u ⟩ ⟨ u |

in Dirac bracket notation. I guess that is like taking an element of the tensor product $H \otimes H^{*}$ .
This formula can be generalized for a projection on a subspace $U$ of any dimension $k$ . Choose an orthonormal basis of $U$ , and take their coordinates with respect to the main orthonormal basis to form a matrix $A$ . Then

P = A \cdot A^{*}