Quantum field

The field approach

Following Sean Carroll in this video.
Quantum field theory is a subset of Quantum Mechanics. We can have a QM theory, with wavefunctions representing the sate of the system and so on, for something discrete, like spin, or for something continuous, like $x$ position. What it is called Quantum Field Theory is a QM theory in which the wavefunctions are fed with classical field configurations. For example, if we have a field $ϕ (x)$ , the wavefunction

Ψ [ϕ (x)]

is a complex number (probability amplitude) whose squared modulus is the probability of measuring the field with precisely the configuration $ϕ (x)$ over the whole space. Of course this measurement doesn't happen ir real life, is an idealization.
More specifically, if $F (R^{3})$ is the set of all functions (field configurations), we have

Ψ : F (R^{3}) \to C .

Particle approach

Source: this eigenchris video.
Coming from coupled quantum harmonic oscillators we have operators ${\hat{x}}_{1}$ and ${\hat{x}}_{2}$

meaning the displacement of every oscillator with respect to the equilibrium position. We have a basis of eigenstates

| x_{1}, x_{2} ⟩ \in H = H_{1} \otimes H_{2},

which corresponds to definite positions for both oscillators. We have that ${\hat{x}}_{1} | x_{1}, x_{2} ⟩ = x_{1} | x_{1}, x_{2} ⟩$ and ${\hat{x}}_{2} | x_{1}, x_{2} ⟩ = x_{2} | x_{1}, x_{2} ⟩$ , where we are abusing of notation since the operators should be ${\hat{x}}_{i} \otimes i d$ .
If we add oscillators, indeed, a continuous amount of them, we obtain a quantum field
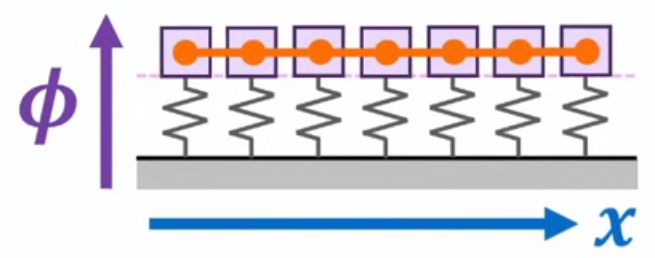
Pasted image 20241214173100.png|600
where now $ϕ$ is the displacement and $x$ is the label for every oscillator. Every $\hat{ϕ} (x)$ is an operator like ${\hat{x}}_{i}$ , and

| ϕ (x) ⟩ \in H

is a basis of eigenstates with definite value $ϕ (x)$ for the oscillator in $x$ . The Hilbert space $H$ is somewhat similar to a "continuous tensor product" of $H$ with itself.
Finally, $\hat{ϕ} (x) | ϕ (x) ⟩ = ϕ (x) | ϕ (x) ⟩$ . Observe that, indeed, we have the same abuse of notation, something like

\hat{ϕ} (x) \Rightarrow \cdot \cdot \cdot 1 \otimes \hat{ϕ} (x) \otimes 1 \cdot \cdot \cdot

So in the same way that we can start with classical several coupled oscillators and go to coupled quantum harmonic oscillators, we could start with the continuous limit of classical coupled oscillators, that is, the Klein--Gordon field, and quantize it. From here we take the Hamiltonian density

H = \frac{π (x)^{2}}{2} + \frac{1}{2} {(\frac{\partial ϕ (x)}{\partial x})}^{2} + \frac{1}{2} m^{2} ϕ (x)^{2},

of the Klein--Gordon field, and we can quantize it to obtain

\hat{H} = \frac{\hat{π} (x)^{2}}{2} + \frac{1}{2} {(\frac{\partial \hat{ϕ} (x)}{\partial x})}^{2} + \frac{1}{2} m^{2} \hat{ϕ} (x)^{2} .

Erroneously, this was called second quantization, since it looked like if you had quantized the energy-momentum relation to obtain the Klein--Gordon equation, and then you quantize again. But indeed you only quantize once, the Hamiltonian of the continuous limit of coupled oscillators.

Old stuff
In a Classical Field Theory every point in space (or spacetime) has a field value. In the corresponding Quantum Field Theory, every point in space/spacetime has an operator associated to it. Unlike in Quantum Mechanics, position is not an operator, but a label for the space.

A field itself, either in classical physics or in its quantization, is simply a function on spacetime, assigning to each spacetime point the "value" of that field at that point. Or rather, more generally it is a section of a bundle over spacetime manifold.
In case of a quantum field, the field operators $ϕ (x)$ at different spacetime points $x$ are different operators, but they all act on the same underlying Hilbert space.
There is a single, fixed Hilbert space of states, on which all the operators $ϕ (x)$ act, not a different Hilbert space for each $x$ . The Hilbert space in question is usually a Fock space, which is a direct sum of tensor product spaces, each one corresponding to a certain number of particles. The Hilbert space provides the "stage" on which all these operators act, and it's constructed to be rich enough to accommodate all the phenomena we wish to describe, such as particle interactions, creation, and annihilation.
According to Susskind (here and better here), a quantum field is a linear combination

Ψ (x) = \sum_{i} a_{i}^{-} ψ_{i} (x)

where:

${| ψ_{i} ⟩}$ is an orthonormal basis of eigenstates for the Hamiltonian $\hat{H}$ of a certain 1-particle system.
$ψ_{i} (x) = ⟨ x | ψ_{i} ⟩$ are the wavefunctions of these states
$a_{i}^{-}$ is the annihilation operator which operates on the Fock space.

According to this derivation of Susskind
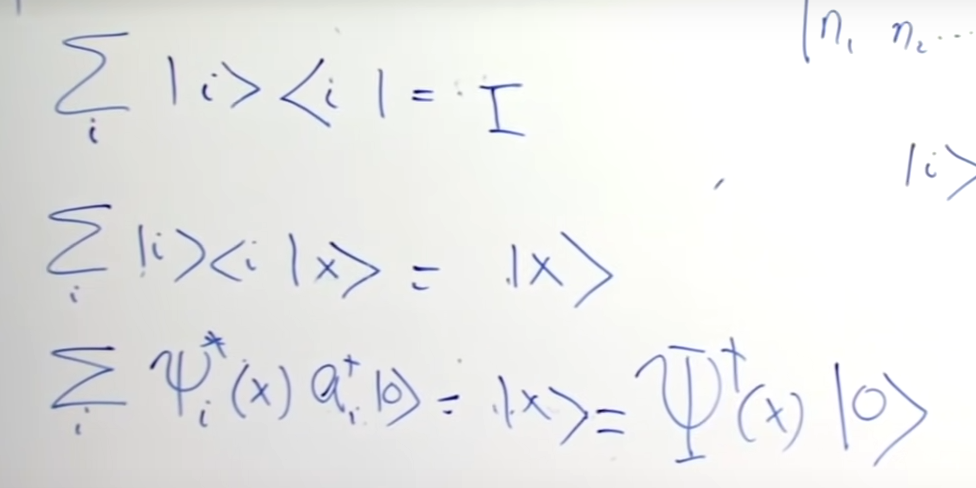
Pasted image 20240118160315.png
the quantum field or, better said, its Hermitian conjugate $Ψ^{†} (x)$ , when applied to the empty state $| 0 ⟩$ , it creates a single particle localized at position $x$ .
Similarly,

Ψ^{†} (y) Ψ^{†} (x) | 0 ⟩

is a two particle state, one at $x$ and one at $y$ .

Moreover, here Susskind shows that $\int d x Ψ^{†} (x) Ψ (x) = \sum_{i} N_{i}$ , where $N_{i}$ is the number operator. So this integral represents an operator which gives us, when applied to a state, the total number of particles. Therefore, $Ψ^{†} (x) Ψ (x)$ represents the "particle density", and it can be measured. Indeed, it is $\int_{R} d x Ψ^{†} (x) Ψ (x)$ , with $R$ a small region of space, what can be measured.

Also, he shows that in case that $ω_{i}$ is the eigenvalue associated to $ψ_{i}$ , then

\hat{E} := \int d x Ψ^{†} (x) \hat{H} Ψ (x) = \sum_{i} N_{i} ω_{1}

where $\hat{H}$ is the Hamiltonian of the 1-particle system. So the operator $\hat{E}$ is the Hamiltonian of the quantum field theory.