Quantum harmonic oscillator

The quantum harmonic oscillator is a fundamental model in quantum mechanics due to its wide applicability in physics, from simple models of atoms to quantization of fields in quantum field theory. The oscillator's energy levels are quantized, and this can be elegantly described using ladder operators.

Mathematical description

First, consider the time-independent Schrödinger equation for the harmonic oscillator:

\hat{H} ψ (x) = E ψ (x)

where $\hat{H}$ is the Hamiltonian operator:

\begin{matrix} (1) & \hat{H} = \frac{{\hat{p}}^{2}}{2 m} + \frac{1}{2} m ω^{2} {\hat{x}}^{2} \end{matrix}

and $\hat{p}$ and $\hat{x}$ are the momentum and position operators, respectively. We should solve the PDE above to find the energy states of the quantum harmonic oscillator (see Schrodinger equation), but this method is very complicated.

Alternatively, we can introduce the ladder operators $\hat{a}$ and ${\hat{a}}^{†}$ (also known as annihilation and creation operators, and lowering and raising operators, respectively) are introduced as:

\hat{a} = \sqrt{\frac{m ω}{2 ℏ}} (\hat{x} + \frac{i \hat{p}}{m ω}), {\hat{a}}^{†} = \sqrt{\frac{m ω}{2 ℏ}} (\hat{x} - \frac{i \hat{p}}{m ω})

These operators satisfy:

\hat{H} = ℏ ω ({\hat{a}}^{†} \hat{a} + \frac{1}{2}) .

Also, they obey the commutation relation $[\hat{a}, {\hat{a}}^{†}] = 1$ . Moreover, $[\hat{H}, {\hat{a}}^{†}] = ℏ ω {\hat{a}}^{†}$ . So we can prove that, if $| E ⟩$ is a state of definite energy $E$ , i.e. $\hat{H} | E ⟩ = E | E ⟩$ , then ${\hat{a}}^{†} | E ⟩$ is an eigenvector for $\hat{H}$ with eigenvalue $E + ℏ ω$ :

\hat{H} {\hat{a}}^{†} | E ⟩ = [\hat{H}, {\hat{a}}^{†}] | E ⟩ + {\hat{α}}^{†} \hat{H} | E ⟩ = ℏ ω {\hat{a}}^{†} | E ⟩ + {\hat{a}}^{†} E | E ⟩ = (E + ℏ ω) | E ⟩

and also $\hat{a} | E ⟩$ is an eigenvector for $\hat{H}$ with eigenvalue $E - ℏ ω$ .
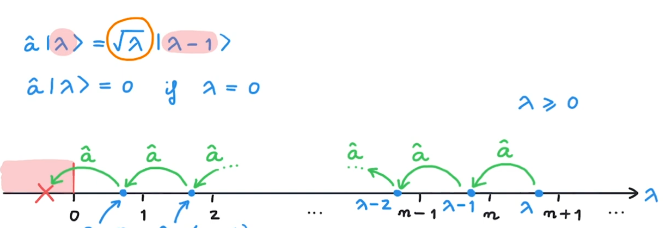
We can construct a "ladder" of energy states by repeatedly applying ${\hat{a}}^{†}$ or $\hat{a}$ . Here, then, is a wonderful machine for generating new solutions, with higher and lower energies—if we could just find one solution, to get started!

Crucially, the energy cannot be negative, according to $(1)$ , so there must be a lowest energy state such that further application of $\hat{a}$ yields zero. This state, denoted by $| 0 ⟩$ , and satisfying $\hat{a} | 0 ⟩ = 0$ , is the ground state. It has the energy $E_{0} = \frac{1}{2} ℏ ω$ , which includes the zero-point energy, the non-zero energy that the oscillator possesses in the ground state due to the Heisenberg uncertainty principle.

This can be shown in another form by defining the number operator $\hat{N} = {\hat{a}}^{†} \hat{a}$ . The eigenstates of $\hat{N}$ are the same as the eigenstates of $\hat{H}$ ( but not with the same eigenvalue). Let's call them $| λ ⟩$ to the normalized eigenvector of eigenvalue $λ$ of $\hat{N}$ , up to a phase factor (there is not only one normalized eigenvector!). We should employ a different name, let's say $| λ ⟩ ⟩$ , to not be confused with eigenvalues of $\hat{H}$ , but we are going to abuse of notation. Now observe that

⟨ λ | \hat{N} | λ ⟩ = λ ⟨ λ | λ ⟩ = λ

and

⟨ λ | \hat{N} | λ ⟩ = (⟨ λ | {\hat{a}}^{†}) (\hat{a} | λ ⟩) = | | \hat{a} | λ ⟩ | |^{2} \geq 0

from where we conclude $λ \geq 0$ .

Since $\hat{N} = \frac{1}{ℏ ω} \hat{H} - 1 / 2$ , we have $[\hat{N}, {\hat{a}}^{†}] = {\hat{a}}^{†}$ , and then $\hat{N} {\hat{a}}^{†} | λ ⟩ = (λ + 1) {\hat{a}}^{†} | λ ⟩$ . The analogous happens for $\hat{a} | λ ⟩$ .

Therefore, ${\hat{a}}^{†} | λ ⟩ = α | λ + 1 ⟩$ , which is not normalized unless $| α | = 1$ . Indeed, we know that $⟨ λ | λ ⟩ = 1$ for every $λ$ , so

| α |^{2} = ⟨ λ | \hat{a} {\hat{a}}^{†} | λ ⟩ = ⟨ λ | 1 + {\hat{a}}^{†} \hat{a} | λ ⟩ = λ + 1

And we choose the phase factor for every $| λ ⟩$ such that $α = \sqrt{λ + 1}$ . So we have

{\hat{a}}^{†} | λ ⟩ = \sqrt{λ + 1} | λ + 1 ⟩

and, analogously,

\hat{a} | λ ⟩ = \sqrt{λ} | λ - 1 ⟩ .

Why Discrete Energy Levels:
Pasted image 20231222164341.png
see this video.

Time evolution of energy eigenstates and coherent eigenstates

Energy eigenstates: Schrodinger equation.

Coherent states:
The eigenstates of the annihilation operator, $\hat{a} (| α ⟩) = α | α ⟩$ , where $α \in C$ , are called coherent states. Their time evolution is given by

\begin{aligned} | ψ (0) ⟩ = | α_{0} ⟩ α_{0} = | α_{0} | e^{i φ} \\ | ψ (t) ⟩ = e^{- i ω t / 2} | α ⟩, where α = α_{0} e^{- i ω t} \end{aligned}

(see this video)

Comparison with classical harmonic oscillator.

Description	Classical Harmonic Oscillator	Quantum Harmonic Oscillator (initial Coherent State $α_{0}$ )
Position $x (t)$	$x_{0} \cos (ω t - φ)$	$\sqrt{\frac{2 ℏ}{m ω}} \| α_{0} \| \cos (ω t - φ)$
Momentum $p (t)$	$- m ω x_{0} \sin (ω t - φ)$	$- \sqrt{2 m ℏ ω} \| α_{0} \| \sin (ω t - φ)$
Energy $E (t)$	$\frac{1}{2} m ω^{2} x_{0}^{2}$	$\hbar\omega \left( \|\alpha_0\|

\frac{1}{2}\right)$ |

The energy for the quantum case includes the contribution from the zero-point energy $\frac{1}{2} ℏ ω$ , which is absent in the classical case.

Two coupled quantum harmonic oscillators

Source: eigenchris video.

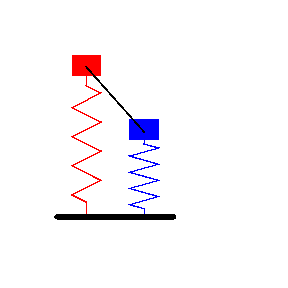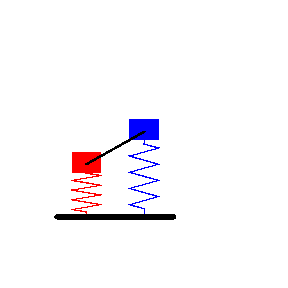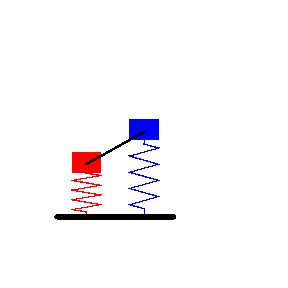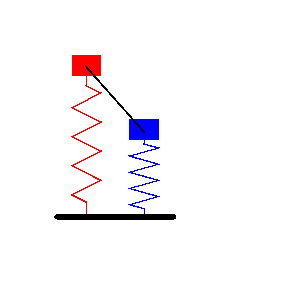
The states live in a tensor product Hilbert space:

| Ψ (t) ⟩ \in H_{1} \otimes H_{2} $ $ w i t h b a s i s o f p o s i t i o n g i v e n b y

|x_1, x_2\rangle = |x_1\rangle \otimes |x_2\rangle

T h e o p e r a t o r s o f t h e i n d i v i d u a l o s c i l l a t o r s p r o m o t e t o n e w o p e r a t o r s :

\hat{x}_1 \implies \hat{x}_1 \otimes 1 \qquad \hat{x}_2 \implies 1 \otimes \hat{x}_2

\hat{p}_1 \implies \hat{p}_1 \otimes 1 \qquad \hat{p}_2 \implies 1 \otimes \hat{p}_2

T h e H a m i l t o n i a n i s

\hat{H} = \frac{\hat{p}_1^2}{2m} + \frac{1}{2}k\hat{x}_1^2
+ \frac{\hat{p}_2^2}{2m} + \frac{1}{2}k\hat{x}_2^2
+ \frac{1}{2}\kappa(\hat{x}_2 - \hat{x}_1)^2

W e c a n e x p r e s s i t i n t e r m s o f t h e c o r r e s p o n d i n g L a d d e r O p e r a t o r s w i t h t h e c h a n g e

\hat{x}_i \equiv \sqrt{\frac{\hbar}{2m\omega}}(\hat{a}_i + \hat{a}_i^\dagger), \quad
\hat{p}_i \equiv \frac{i}{\sqrt{2}}\sqrt{\hbar m \omega}(\hat{a}_i - \hat{a}_i^\dagger)

S o t h e H a m i l t o n i a n b e c o m e s :

\hat{H} = \hbar \omega (\hat{a}_1^\dagger \hat{a}_1 + \hat{a}_2^\dagger \hat{a}_2 + 1)
- \kappa \frac{\hbar}{2m\omega} (\hat{a}_1 + \hat{a}_1^\dagger)(\hat{a}_2 + \hat{a}_2^\dagger)

w h i c h i s s t i l l v e r y c o m p l i c a t e d . I f w e p e r f o r m a v a r i a b l e t r a n s f o r m a t i o n s i n t o n o r m a l m o d e s :

\hat{x}_1 = \frac{1}{\sqrt{2}}(\hat{X}_1 + \hat{X}_2), \quad
\hat{x}_2 = \frac{1}{\sqrt{2}}(\hat{X}_1 - \hat{X}_2)

\hat{p}_1 = \frac{1}{\sqrt{2}}(\hat{P}_1 + \hat{P}_2), \quad
\hat{p}_2 = \frac{1}{\sqrt{2}}(\hat{P}_1 - \hat{P}_2)

w e o b t a i n t h e t r a n s f o r m e d H a m i l t o n i a n :

\hat{H} = \frac{1}{2m}\hat{P}_1^2 + \frac{1}{2}k\hat{X}_1^2
+ \frac{1}{2m}\hat{P}_2^2 + \frac{1}{2}(k + 2\kappa)\hat{X}_2^2

w h i c h c o r r e s p o n d s t o t w o d e c o u p l e d q u a n t u m h a r m o n i c o s c i l l a t o r s . W e c a n u s e n o w t h e c o r r e s p o n d i n g l a d d e r o p e r a t o r s f o r t h e n o r m a l m o d e s

\hat{X}_i \equiv \sqrt{\frac{\hbar}{2m\Omega_i}}(\hat{A}_i + \hat{A}_i^\dagger), \quad
\hat{P}_i \equiv \frac{i}{\sqrt{2}}\sqrt{\hbar m \Omega_i}(\hat{A}_i - \hat{A}_i^\dagger)

t o o b t a i n t h e H a m i l t o n i a n :

\hat{H} = \hbar \Omega_1 \left(\hat{A}_1^\dagger \hat{A}_1 + \frac{1}{2}\right)
+ \hbar \Omega_2 \left(\hat{A}_2^\dagger \hat{A}_2 + \frac{1}{2}\right)