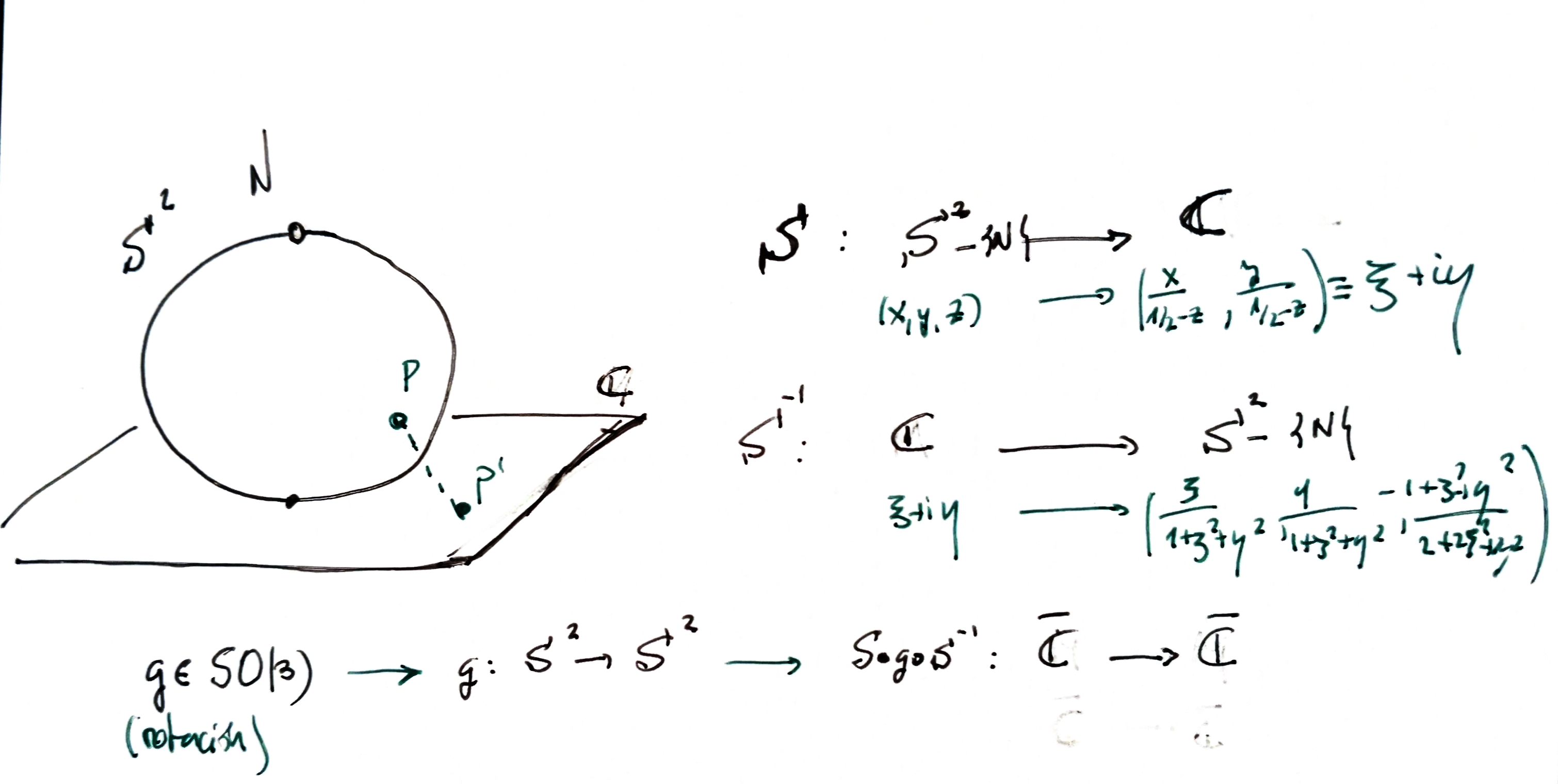
Stereographic projection

There are several conventions:

First approach

If we use a sphere of radius 1 and project from the north pole $N = (0, 0, 1)$ to the plane $z = 0$ the formulas of stereographic projection and its inverse are

\begin{aligned} (ξ, η) & = (\frac{x}{1 - z}, \frac{y}{1 - z}) \\ (x, y, z) & = (\frac{2 ξ}{1 + ξ^{2} + η^{2}}, \frac{2 η}{1 + ξ^{2} + η^{2}}, \frac{- 1 + ξ^{2} + η^{2}}{1 + ξ^{2} + η^{2}}) \end{aligned}

where $(ξ, η)$ are coordinates in the plane and $(x, y, z)$ coordinates in $R^{3}$

The sphere has a Riemannian metric inherited by the usual metric of $R^{3}$ , which is translated to the plane $z = 0$ as

(\begin{array}{cc} \frac{4}{(1 + ξ^{2} + η^{2})^{2}} & 0 \\ 0 & \frac{4}{(1 + ξ^{2} + η^{2})^{2}} \end{array})

This metric is conformal to the Euclidean metric, so stereographic projection provide isothermal coordinates for the sphere.

Second approach

If we use a sphere of radius 1/2 and the plane z = −1/2 we have the formulas