Torsion

Definition

Given a manifold with a covariant derivative operator $(M, \nabla)$ , we can define a tensor named torsion as

T (u, v) = \nabla_{u} v - \nabla_{v} u - [u, v]

Or, in Penrose abstract index notation:

T_{a b}^{c} X^{a} Y^{b} = X^{m} \nabla_{m} Y^{c} - Y^{m} \nabla_{m} X^{c} - [X, Y]^{c}

Interpretation

Since we know that the Lie bracket $[u, v]$ measures the fail to close a rectangle along flow lines of $u$ and $v$ , $T (u, v)$ measures the fail to close a rectangle made of parallel transported vectors along the flow, as you can observe in the picture (taken from here):
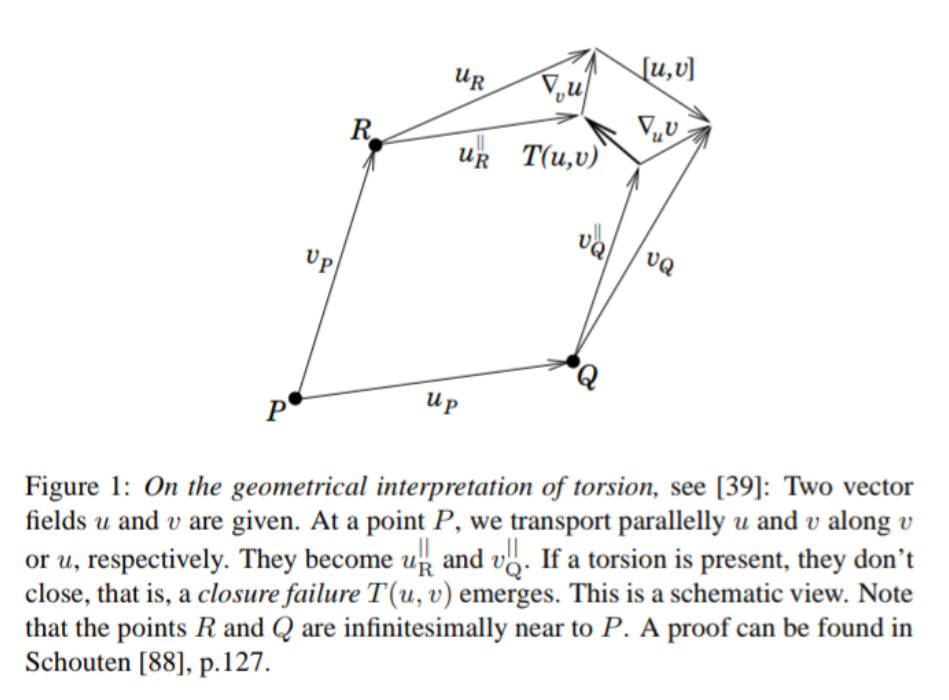
Pasted image 20220703105722.png
Personal thought: I think it should be defined independently of the Lie bracket, in a way that reflects more intrinsically the idea of "the fail to close a rectangle made of parallel transported vectors along the flow".
Explanation (see better relation of Lie derivative, covariant derivative and torsion): observe that, as it has been said here,

\nabla_{u} v = lim_{ϵ \to 0} \frac{(v_{Q})_{∥} (Q \to P) - v_{P}}{ϵ} =

= lim_{ϵ \to 0} \frac{v_{Q} - (v_{P})_{∥} (P \to Q)}{ϵ} ≍ \frac{v_{Q} - (v_{P})_{∥} (P \to Q)}{ϵ}

and so

\nabla_{ϵ u} v ≍ v_{Q} - (v_{P})_{∥} (P \to Q)

In the (schematic) picture above, since $Q$ is considered infinitesimally near to $P$ , this is translated as

\nabla_{u} v = v_{Q} - v_{Q}^{∥}

And analogously

\nabla_{v} u = u_{R} - u_{R}^{∥}

On the other hand, observe that according to this, we have

[u, v] ≍ u_{P} + v_{Q} - (v_{P} + u_{R})

and therefore the quantity

T (u, v) = \nabla_{u} v - \nabla_{v} u - [u, v] ≍

≍ v_{Q} - v_{Q}^{∥} - (u_{R} - u_{R}^{∥}) - (u_{P} + v_{Q} - (v_{P} + u_{R})) =

= v_{P} + u_{R}^{∥} - (u_{P} + v_{Q}^{∥}),

which is the gap of the parallelogram made of parallel transported vectors (along infinitesimally short curves $P Q$ and $P R$ !). This can be fully formalized working in a local chart and using Taylor expansion (see xournal_166).

Almost always, the given connection is torsion free (for example, the Levi-Civita connection). So it turns out that

[u, v] = \nabla_{u} v - \nabla_{v} u

Expression in coordinates

It can be shown that for any connection, in coordinates,

T_{i j}^{k} = Γ_{i j}^{k} - Γ_{j i}^{k}

i.e., the difference of the Christoffel symbols, in case it is the Levi-Civita connection.
Since it is a torsion free connection, Christoffel symbols are symmetric.