Variational bicomplex

It is a double complex defined in order to formalize Classical Field Theory, specifically Lagrangian field theory.

Consider the infinite jet bundle $J^{\infty} (E)$ . We have that the Cartan distribution, or its dual expression the contact ideal, let us decompose

Ω^{p} (J^{\infty} (E)) = ⨁_{r + s = p} Ω^{r, s} (J^{\infty} (E))

where $ω \in Ω^{r, s} (J^{\infty} (E))$ if it is the sum of terms of the form

f [u] d x^{i_{1}} \land \dots \land d x^{i_{r}} \land θ_{J_{1}}^{α_{1}} \land \dots \land θ_{J_{s}}^{α_{s}}

with $θ_{I}^{α}$ the contact forms (see Anderson_1992).
The exterior derivative

d : Ω^{p} (J^{\infty} (E)) \to Ω^{p + 1} (J^{\infty} (E))

splits

d = d_{H} + d_{V}

where

\begin{array}{l} d_{H} : Ω^{r, s} (J^{\infty} (E)) \to Ω^{r + 1, s} (J^{\infty} (E)) \\ d_{V} : Ω^{r, s} (J^{\infty} (E)) \to Ω^{r, s + 1} (J^{\infty} (E)) \end{array}

Since $d^{2} = 0$ and the decomposition is a direct sum we have that

d_{H}^{2} = 0

d_{H} d_{V} = - d_{v} d_{H}

d_{V}^{2} = 0

The double complex $(Ω^{*, *} (J^{\infty} (E)), d_{H}, d_{V})$ is called the variational bicomplex.
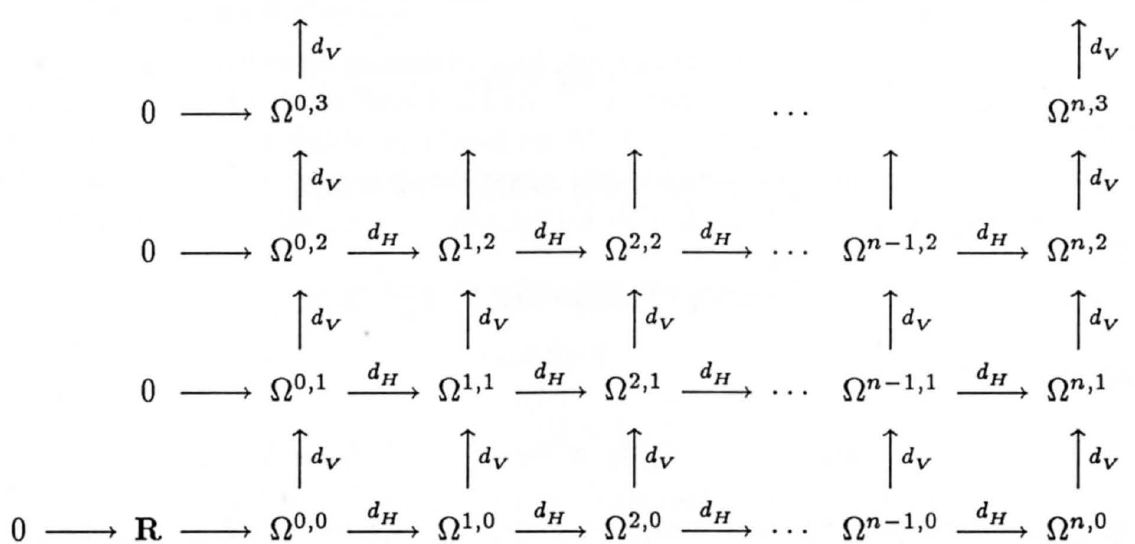
Pasted image 20220421162327.png

A form $λ \in Ω^{n, 0}$ is a Lagrangian for a variational problem. See also Euler operator and Helmholtz operator.