Relationship between $S O (3)$ and $S U (2)$

High technology approach

The special orthogonal group SO(3) consists of rotations of the 3D space. It can be defined in several ways, but ultimately we have a group representation

S O (3) ⟶ G L (R^{3})

This way, $S O (3)$ corresponds to orthogonal matrices with determinant equal to 1.

The Lie algebra $s o (3)$ corresponds, by means of this representation, to antisymmetric matrices

[\begin{array}{ccc} 0 & - c & b \\ c & 0 & - a \\ - b & a & 0 \end{array}] \leftrightarrow (a, b, c) \in R^{3}

with generators

\hat{x} = [\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & - 1 \\ 0 & 1 & 0 \end{array}], \hat{y} = [\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ - 1 & 0 & 0 \end{array}], \hat{z} = [\begin{array}{ccc} 0 & - 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array}]

On the other hand, we have the group SU(2), of unitary 2x2 complex matrices with determinant equal to 1. This definition is, in fact, a complex linear representation by itself

S U (2) ⟶ G L (C^{2}) .

The Lie algebra $s u (2)$ consists of anti-hermitian matrices (see Hermitian matrix) with null trace, and has a basis

e_{1} = [\begin{array}{cc} 0 & i \\ i & 0 \end{array}]; e_{2} = [\begin{array}{cc} 0 & - 1 \\ 1 & 0 \end{array}]; e_{3} = [\begin{array}{cc} i & 0 \\ 0 & - i \end{array}]

(by the way, these are the Pauli matrices multiplied by $i$ ).
The Lie algebras $s o (3)$ and $s u (2)$ not only have the same dimension, but they are isomorphic: we can map

\begin{matrix} \hat{x} \mapsto \frac{1}{2} e_{1} \\ \hat{y} \mapsto \frac{1}{2} e_{2} \\ \hat{z} \mapsto \frac{1}{2} e_{3} \end{matrix}

and conserve the commutation relations.

Since $S O (3)$ and $S U (2)$ have the same Lie algebra, they have the same universal covering (in particular SU(2) is a double cover of $S O (3)$ ). And since $S U (2)$ is simply connected (because it is diffeomorphic to $S^{3}$ , see section unitary matrix#What is SU 2 topologically), it is the universal covering group of $S O (3)$ .

Low level approach

But we can forget about these sophisticated tools, and try to see more directly the relationship between $S U (2)$ and $S O (3)$ .The idea follows this way:

$S O (3)$ can be seen like rotations of a sphere $S^{2}$ .
Therefore, they can be seen like some kind of transformations of the extended complex plane $\bar{C}$ , via stereographic projection $S : S^{2} \mapsto \bar{C}$ . They constitute a subgroup of Moebius transformations $M$ , since they are conformal maps (rotations are conformal, and stereographic projection is).
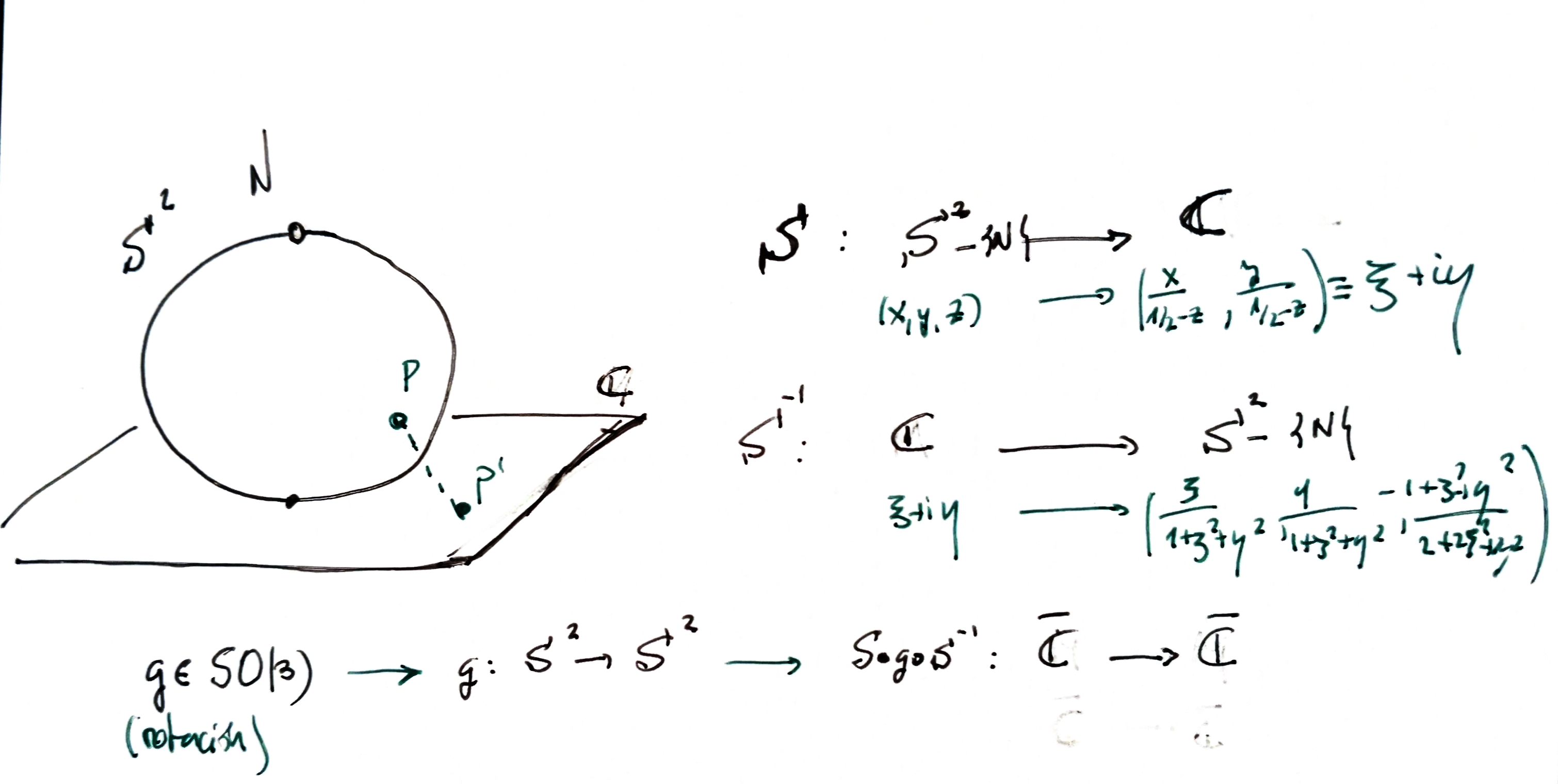
But $M$ is, in fact, the same as the group $P G L (2, C) = G L (2, C) / {λ I}$ acting over $C P^{1}$ . This identification comes this way: the Moebius transformation

z \mapsto \frac{a z + b}{c z + d}

with $a d - b c \neq 0$ corresponds to

[(\begin{array}{ll} a & b \\ c & d \end{array})] \in G L (2, C) / {λ I}

with nonzero determinant.

In other words, the complex vector space $C^{2}$ gives rise to the complex projective line (aka the Riemann sphere). The linear transformations of $C^{2}$ give rise to Mobius transformations.

But several linear transformations give rise to the same Moebius transformation, so we take equivalence classes. Even if we restrict to the singular matrices with unit determinant, we have a 2-1 relation. That is, we have a 2-1 surjection from $S L (2, C)$ to the group of Moebius, $M$ . That is,

M \equiv G L (2, C) / {λ I} \equiv S L (2, C) / {\pm I}

so we can express the Moebius transformation (abusing of notation) by

\pm (\begin{array}{ll} a & b \\ c & d \end{array})

with $a d - b c = 1$ .

To see which Moebius transformations correspond to which rotations, let's study two of them: rotation along the $z$ -axis and angle $ϕ$ ,

R_{z}^{ϕ} \equiv {\begin{cases} x^{'} = x \cos ϕ - y \sin ϕ \\ y^{'} = x \sin ϕ + y \cos ϕ \\ z^{'} = z \end{cases}

and rotation along the $x$ -axis and angle $θ$ ,

R_{x}^{θ} \equiv {\begin{cases} x^{'} = x \\ y^{'} = y \cos θ - z \sin θ \\ z^{'} = y \sin θ + z \cos θ \end{cases}

Pure algebraic manipulations lead us to the Moebius transformations:

r_{z}^{ϕ} = S R_{z}^{ϕ} S^{- 1} \equiv ζ \mapsto \frac{e^{\frac{i ϕ}{2}} ζ + 0}{0 ζ + e^{- \frac{i ϕ}{2}}}

and

r_{x}^{θ} = S R_{x}^{θ} S^{- 1} \equiv ζ \mapsto \frac{\cos \frac{θ}{2} ζ + i \sin \frac{θ}{2}}{i \sin \frac{θ}{2} ζ + \cos \frac{θ}{2}}

so, in $S L (2, C) / {\pm I}$

r_{z}^{ϕ} = \pm (\begin{array}{cc} e^{i \frac{ϕ}{2}} & 0 \\ 0 & e^{- i \frac{ϕ}{2}} \end{array})

r_{x}^{θ} = \pm (\begin{array}{cc} \cos \frac{θ}{2} & i \sin \frac{θ}{2} \\ i \sin \frac{θ}{2} & \cos \frac{θ}{2} \end{array})

Now, a general rotation $R$ is a composition of the two above (see section on Euler angles), so the same is true for the associated Moebius transformation.
So if we start with the rotation of Euler angles $ϕ, θ, ψ$ :

R = R_{ϕ, θ, ψ} = (\begin{array}{ccc} \cos ϕ & - \sin ϕ & 0 \\ \sin ϕ & \cos ϕ & 0 \\ 0 & 0 & 1 \end{array}) (\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos θ & - \sin θ \\ 0 & \sin θ & \cos θ \end{array}) (\begin{array}{ccc} \cos ψ & - \sin ψ & 0 \\ \sin ψ & \cos ψ & 0 \\ 0 & 0 & 1 \end{array}) =

= (\begin{array}{ccc} \cos ϕ \cos ψ - \cos θ \sin ϕ \sin ψ & - \cos ϕ \sin ψ - \cos θ \sin ϕ \cos ψ & \sin ϕ \sin θ \\ \sin ϕ \cos ψ + \cos θ \cos ϕ \sin ψ & - \sin ϕ \sin ψ + \cos θ \cos ϕ \cos ψ & - \cos ϕ \sin θ \\ \sin ψ \sin θ & \cos ψ \sin θ & \cos θ \end{array})

we get

r_{ϕ, θ, ψ} = \pm (\begin{array}{cc} e^{i \frac{ϕ}{2}} & 0 \\ 0 & e^{- i \frac{ϕ}{2}} \end{array}) (\begin{array}{cc} \cos \frac{θ}{2} & i \sin \frac{θ}{2} \\ i \sin \frac{θ}{2} & \cos \frac{θ}{2} \end{array}) (\begin{array}{cc} e^{i \frac{ψ}{2}} & 0 \\ 0 & e^{- i \frac{ψ}{2}} \end{array})

= \pm (\begin{array}{cc} \cos \frac{θ}{2} e^{i \frac{ϕ + ψ}{2}} & i \sin \frac{θ}{2} e^{i \frac{ϕ - ψ}{2}} \\ i \sin \frac{θ}{2} e^{- i \frac{ϕ - ψ}{2}} & \cos \frac{θ}{2} e^{- i \frac{ϕ + ψ}{2}} \end{array})

where the determinant is obviously 1.

You can check that all the matrices like above are of the form

\pm (\begin{array}{cc} α & β \\ - \bar{β} & \bar{α} \end{array})

with $| α |^{2} + | β |^{2} = 1$ , that is, it belong to $S U (2) / {\pm I}$ . But the converse is also true. Every such pair of matrices in $S U (2)$ comes from a Moebius transformation corresponding to a rotation. To see that, we only have to solve

\begin{aligned} \cos \frac{θ}{2} & = | α |, \sin \frac{θ}{2} = | β |, (0 \leq θ \leq π) \\ \frac{ϕ + ψ}{2} & = \arg α, \frac{ψ - ϕ}{2} = \arg β \end{aligned}

to find the Euler angles.
We can even express the 3x3 rotation matrix in function of the given complexes numbers:

(\begin{array}{ccc} \frac{1}{2} (α^{2} - β^{2} + \overset{―}{α^{2}} - \overset{―}{β^{2}}) & \frac{i}{2} (- α^{2} - β^{2} + \overset{―}{α^{2}} + \overset{―}{β^{2}}) & - α β - \bar{α} \bar{β} \\ \frac{i}{2} (α^{2} - β^{2} - \overset{―}{α^{2}} + \overset{―}{β^{2}}) & \frac{1}{2} (α^{2} + β^{2} + \overset{―}{α^{2}} + \overset{―}{β^{2}}) & - i (+ α β - \bar{α} \bar{β}) \\ α \bar{β} + \bar{α} β & i (- α \bar{β} + \bar{α} β) & α \bar{α} - β \bar{β} \end{array})

So we have a surjective 2-1 group homomorphism

π : S U (2) ⟼ S O (3)

with kernel ${\pm I}$ . I.e., $S U (2)$ is a double cover of $S O (3)$ .

Relationship between SO(3) and SU(2)

High technology approach

Low level approach

Relationship between $S O (3)$ and $S U (2)$