Context: Classical Statistical Mechanics.
Handwritten: [[temperature-ideas.pdf]]

1. Entropy Alone: A Measure of Uncertainty

First, let's consider a system where energy plays no role.
Imagine a 6x8 grid of 48 holes and 4 indistinguishable balls. We assume all 48 holes are equal—it "costs" nothing to put a ball in any hole, and no arrangement is "better" or "worse" than any other. And no hole can hold more than one ball.

Because all arrangements are equally likely, the only meaningful question we can ask is: "How many total ways can we arrange the 4 balls in the 48 holes?"

This is a combinations problem:

• Microstates ($W$): The total number of possible, distinct arrangements.

Entropy ($H$) is the measure of our uncertainty about this system. If we pick up the box and shake it, we know it will settle into one of these 194,580 microstates. Our uncertainty is given by the number of "yes/no" questions (bits) it would take to find the exact arrangement (see Shannon entropy).

In this context, entropy is just a single, fixed number. It doesn't change. It simply describes the total statistical complexity of the system's "state space". There is no concept of temperature here.

2. Introducing Energy: The Vertical Grid

Now, let's change the rules. Temperature can only enter the scene when different microstates have different energies. Let's swap our flat grid for a vertical 6x8 grid. We still have 4 balls and 48 holes, but the holes are now on different rows, each with an energy "cost".

• Row 1 (Bottom): Energy cost = 1 unit. Has 8 spots.
• Row 2: Energy cost = 2 units. Has 8 spots.
• Row 3: Energy cost = 3 units. Has 8 spots.
• Row 4: Energy cost = 4 units. Has 8 spots.
• Row 5: Energy cost = 5 units. Has 8 spots.
• Row 6 (Top): Energy cost = 6 units. Has 8 spots.

The total number of ways to put 4 balls in 48 spots is still a fixed number ($(\genfrac{}{}{0ex}{}{48}{4})$), but this number is no longer very useful. Why? Because the system's behavior will be limited by its total energy.

The important question is no longer "How many total arrangements exist?"
The new question is: "How many arrangements ($W$) exist for a specific total energy $E$?"

Case 1: System with Total Energy E = 4

Let's find $W(E=4)$, the number of ways to arrange the 4 balls to get a total energy of exactly 4 units.

• The only possible arrangement is to place all 4 balls on Row 1.
  • Energy Check: $4\text{ balls}\times 1\text{ unit/ball}=4\text{ units}$. This works.
• How many microstates? We must choose 4 spots from the 8 available on Row 1.
  • $W(E=4)=(\genfrac{}{}{0ex}{}{8}{4})=70$ microstates.

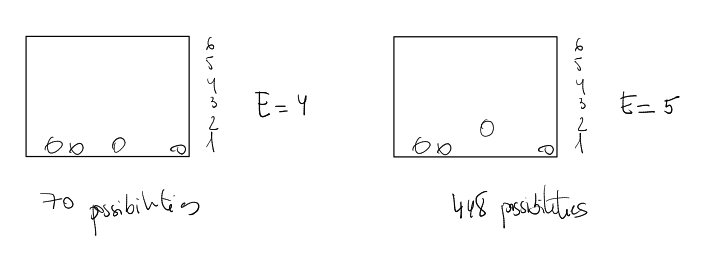
Case 2: System with Total Energy E = 5

Now, let's add 1 unit of energy to the system. Our new total energy is $E=5$.

• The only possible arrangement is 3 balls on Row 1 and 1 ball on Row 2.
  • Energy Check: $(3\text{ balls}\times 1\text{ unit})+(1\text{ ball}\times 2\text{ units})=5\text{ units}$. This works.
• How many microstates? We choose 3 spots from 8 (Row 1) AND 1 spot from 8 (Row 2).
  • $W(E=5)=(\genfrac{}{}{0ex}{}{8}{3})\times (\genfrac{}{}{0ex}{}{8}{1})=56\times 8=448$ microstates.

3. How This Defines Temperature

Look at what just happened. The number of available microstates ($W$) is not a fixed number; it depends on the energy $E$.

• $W(E=4)=70$
• $W(E=5)=448$

This is the key. Thermodynamic entropy ($S$) is defined as the logarithm of this energy-dependent number.

This means entropy itself is a function of energy.

• $S(E=4)=k_B\ln (70)$
• $S(E=5)=k_B\ln (448)$
  
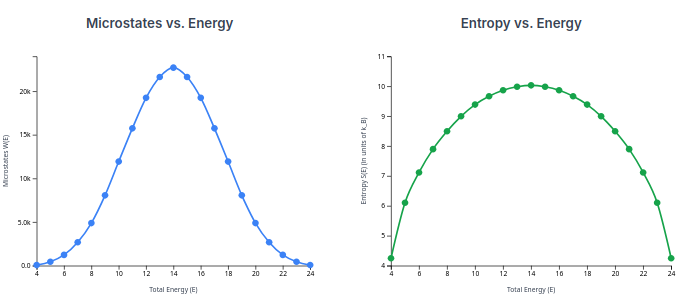
  Since $S$ changes when $E$ changes, we can measure its rate of change (its derivative). That rate of change is the fundamental definition of Temperature ($T$) or coolness ($\beta$).

This formula tells us the physical meaning of temperature:

• Low Temperature ($T$ is small): This means $\frac{1}{T}$ (the rate of change $\frac{\partial S}{\partial E}$) is large. This describes a system where adding a little energy (like going from E=4 to E=5) "unlocks" a huge number of new states (from 70 to 448). The system is "starved" for energy, and its entropy is highly sensitive to adding more.

• High Temperature ($T$ is large): This means $\frac{1}{T}$ (the rate of change $\frac{\partial S}{\partial E}$) is small. This describes a system that is already "saturated" with energy. Adding one more unit of energy might open up some new states, but the proportional increase is tiny. The system's entropy is not very sensitive to new energy.

4. Connecting to Our Daily Lives: "Hot" vs. "Cold"

This abstract definition perfectly explains our daily experience. The bridge is the second law of thermodynamics: when two systems interact, the total entropy of the combined system must increase.
When you touch a cold can of soda, heat flows from your hand to the can. Why?

• A "Cold" Object (Low T): Has a large $\frac{\partial S}{\partial E}$. It is "statistically starved." Adding a little energy (heat) will dramatically increase its entropy.
• A "Hot" Object (High T): Has a small $\frac{\partial S}{\partial E}$. It is "statistically saturated." Losing a little energy (heat) will only slightly decrease its entropy.

Let's see what happens when 1 unit of energy (heat) flows from your "hot" hand to the "cold" can:

• Your Hot Hand (System 1):

  • It loses 1 unit of energy.
  • Because its $\frac{\partial S}{\partial E}$ is small, its entropy decreases by a small amount.
  • $\mathrm{\Delta }{S}_{\text{hand}}=(\text{small negative number})$

• The Cold Can (System 2):

  • It gains 1 unit of energy.
  • Because its $\frac{\partial S}{\partial E}$ is large, its entropy increases by a large amount.
  • $\mathrm{\Delta }{S}_{\text{can}}=(\text{LARGE POSITIVE NUMBER})$

The Net Result for the Universe:
$\mathrm{\Delta }{S}_{\text{total}}=\mathrm{\Delta }{S}_{\text{hand}}+\mathrm{\Delta }{S}_{\text{can}}=(\text{small negative number})+(\text{LARGE POSITIVE NUMBER})=\text{Positive!}$

Because the total entropy of the universe increased, this process is spontaneous and will happen. Heat must flow from hot to cold, as this is the only direction that satisfies the Second Law.

• "Hot" is just our word for a system that will give away energy to increase the universe's total entropy.
• "Cold" is our word for a system that will accept energy to increase the universe's total entropy.
• "Thermal Equilibrium" (two objects at the same temperature) is simply the point where $\frac{\partial S_1}{\partial E_1}=\frac{\partial S_2}{\partial E_2}$, so transferring energy gives zero net change in entropy. Heat flow stops.