Gauss's lemma
@needham2021visual page 274.
On a general surface, if we launch particles in all directions from a point
Lemma
The geodesic circle
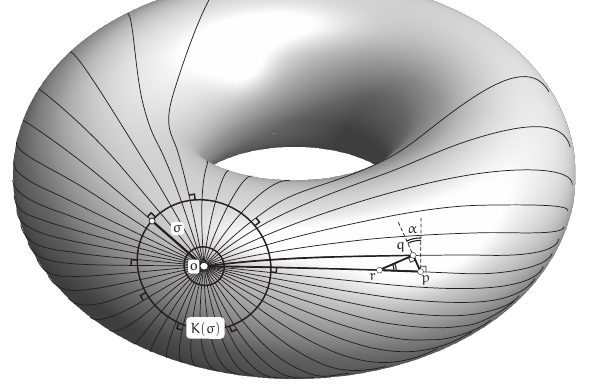
Proof
Idea: suppose
so it cannot be
By a symmetry argument (exchanging the roles of
@needham2021visual page 274.
On a general surface, if we launch particles in all directions from a point
Lemma
The geodesic circle

Proof
Idea: suppose
so it cannot be
By a symmetry argument (exchanging the roles of