Invariants by derivation property for vectors

Given a vector field $A=\partial x+u_1\partial u+\cdots +\varphi \partial u_{m-1}$ encoding an $m$-th order ODE, and $X$ a vector field such that

(that is, a generalized Cinf-symmetry ODE). Then if $w$ and $y$ are differential invariants of $X$ then ${\displaystyle \frac{A(w)}{A(y)}}$ is also a differential invariant.

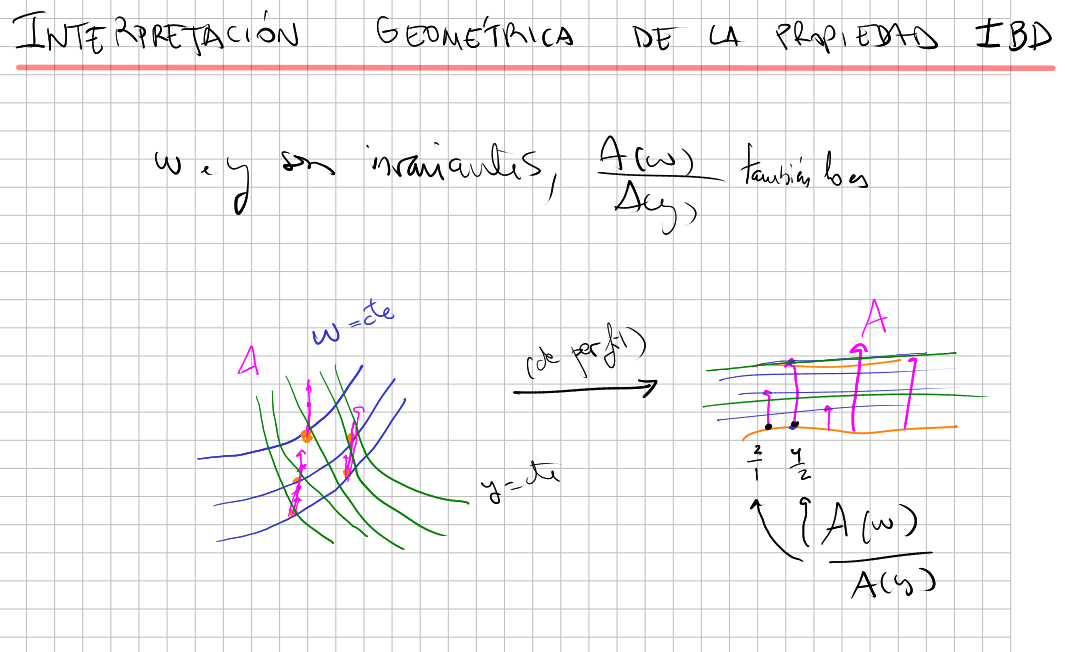
IBD property is also applied to distributions.

It turns out that the vector fields above are the more general class of vector fields satisfying the IBDP (@MR2001541). But, are they independent?