Plank's law

Plank obtained a formula to explain how a body emits different lights depending of its temperature.

u (ν, T) = \frac{8 π h ν^{3}}{c^{3}} (\frac{1}{e^{\frac{h ν}{k T}} - 1})

In this formula:

$u (ν, T)$ is the energy density per unit volume per unit frequency at frequency $ν$ and temperature $T$ .
$h$ is Planck's constant ( $6.62607015 \times 10^{- 34}$ m $^{2}$ kg / s).
$ν$ is the frequency of the electromagnetic radiation.
$c$ is the speed of light in a vacuum ( $3.00 \times 10^{8}$ m/s).
$k$ is Boltzmann's constant ( $1.380649 \times 10^{- 23}$ m $^{2}$ kg s $^{- 2}$ K $^{- 1}$ ). See Boltzmann distribution.
$T$ is the absolute temperature of the black body in kelvins (K).

To understand, first, the problem solved by Plank: video of the ultraviolet catastrophe
In this video also appears the key steps in the reasoning of Plank:
Energy levels are discrete and can be represented as $E = 0, ϵ, 2 ϵ, 3 ϵ, 4 ϵ, \dots$ or $E = n ϵ$ where $n = 1, 2, 3, \dots$
To calculate average energy, replace integrals with sums.
The continuous form for average energy is (taking into account Boltzmann distribution):

\bar{E} = \frac{\int_{0}^{\infty} E e^{- E / k T} d E}{\int_{0}^{\infty} e^{- E / k T} d E}

This is transformed into a discrete sum for quantized energy:

\bar{E} = \frac{\sum_{n = 0}^{\infty} n ϵ e^{- n ϵ / k T}}{\sum_{n = 0}^{\infty} e^{- n ϵ / k T}}

Another derivation of Plank's law, here

Alternative explanation

1. Blackbody radiation

See this video. It can be studied by means of a box with a hole.
boxhole
Inside the box, we have 3-dimensional standing waves at all possible frequencies (well, the corresponding wavelengths must satisfy that an integer number of half-wavelengths fit across each box dimension). In more detail, consider a rectangular box with sides of length $L_{x}$ , $L_{y}$ , and $L_{z}$ . For standing waves, the wavelength $λ$ along each dimension must satisfy boundary conditions that require the electric and magnetic fields to go to zero at the walls. This results in allowed wavelengths of the form:

λ_{x} = \frac{2 L_{x}}{n_{x}}, λ_{y} = \frac{2 L_{y}}{n_{y}}, λ_{z} = \frac{2 L_{z}}{n_{z}}

where $n_{x}$ , $n_{y}$ , and $n_{z}$ are positive integers (1, 2, 3, ...). This means the possible standing wave modes in the box correspond to different combinations of these integers, each combination yielding a specific wavelength and, therefore, a specific frequency.
Each combination $(n_{x}, n_{y}, n_{z})$ gives rise to a unique standing wave pattern with its own frequency $f$ determined by:

f = \frac{c}{λ} = \frac{c}{\sqrt{λ_{x}^{2} + λ_{y}^{2} + λ_{z}^{2}}}

where $c$ is the speed of light, and $λ$ is the resultant wavelength from the combination of the three components.

This quantization in wavelengths means only discrete frequencies are allowed, but in a large box (where $L_{x}$ , $L_{y}$ , and $L_{z}$ are significant), the spacing between these frequencies is very small. Thus, when we examine the energy distribution (especially in the thermal range), it can appear almost continuous.

On the other hand, it was observed that each frequency didn't have the same intensity. Something like this:
blackbody|600

These graphs were empirically constructed.

2. Classical explanation using Maxwell equations

See this video

Equipartition theorem: the equipartition theorem states that, in thermal equilibrium, the total energy of a system is distributed equally among all its degrees of freedom.
Infinite degrees of freedom: we have an infinite number of frequencies, i.e., of degrees of freedom. Indeed, every mode of the frequency is a degree of freedom. As the frequency increases, the number of modes grows (we are in 3 dimensions!), so the energy contribution from these high-frequency modes should also increase indefinitely. In principle, every wavelength can be presented with any energy (only depends on the amplitude, see this other video). The average energy for the wavelength is the same, $E_{0}$ , for every mode of every wavelength. As a result, we have the ultraviolet catastrophe: much more intensity at shorter wavelengths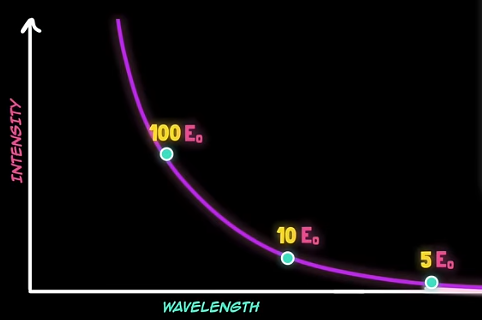

Plank's solution

For every wavelength (or frequency), he assumed that the provided energy is quantized. With a fine quantization, there is no much loss of energy, but for a coarse quantization there is a big loss. So he postulated that the quantization should be proportional to frequency (inverse to wavelength). Graphically: (this video)
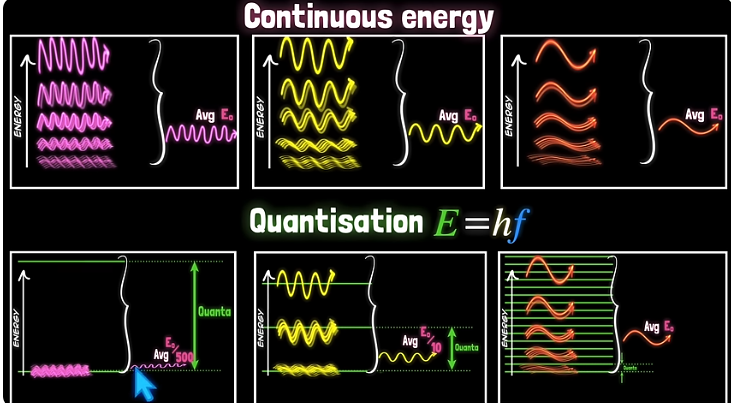
Pasted image 20241031133322.png
So for shorter wavelength the big loss of energy compensate to produce the observed curve, not that predicted by classical physics.

This was only a computational tool, which was explained later by Einstein together with the photoelectric effect.