Hilbert space
It is a vector space equipped with an inner product that is Cauchy complete.
Therefore is a kind of normed space and a Banach space.
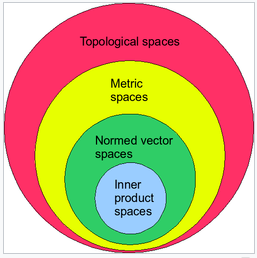
Fundamental result isomorphism between l_2 and L_2.
Examples:
l^2(Z_n)
It is a vector space equipped with an inner product that is Cauchy complete.
Therefore is a kind of normed space and a Banach space.

Fundamental result isomorphism between l_2 and L_2.
Examples:
l^2(Z_n)