The Prime Counting Function $\pi (n)$

• Definition: The prime counting function, denoted $\pi (n)$, counts the number of prime numbers less than or equal to a given number $n$.

• Examples:

  • $\pi (10)=4$, since the primes $\le 10$ are $2,3,5,7$.
  • $\pi (13)=6$, since the primes $\le 13$ are $2,3,5,7,11,13$.

• Nature: $\pi (n)$ is a step function — it increases by 1 exactly at each prime number.

• Mathematical Interest: A key goal in analytic number theory is to understand how fast $\pi (n)$ grows as $n\to \mathrm{\infty }$.

Approximations:

• prime number theorem.
• the logarithmic integral

Related:

• Chebyshev function

Dream of a Formula

In this video it is presented the (informal) idea of a Riemann converter or Riemann harmonics:

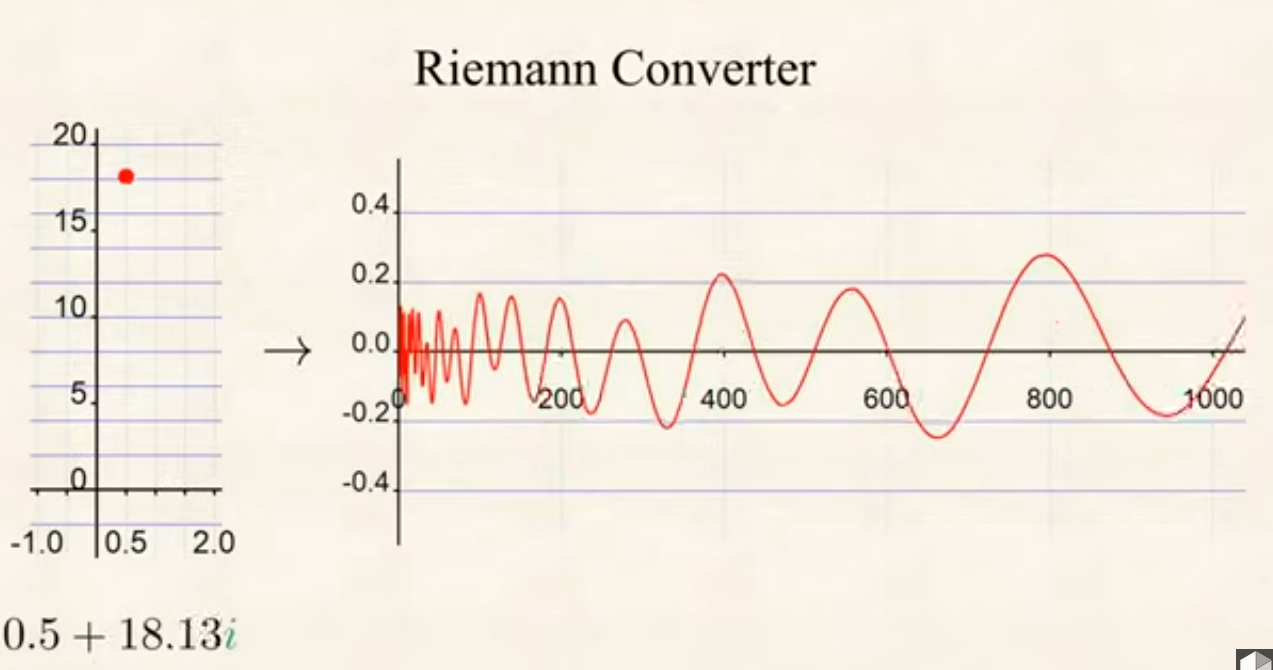
Each non-trivial zero can be seen as a kind of oscillatory function, in such a way that:

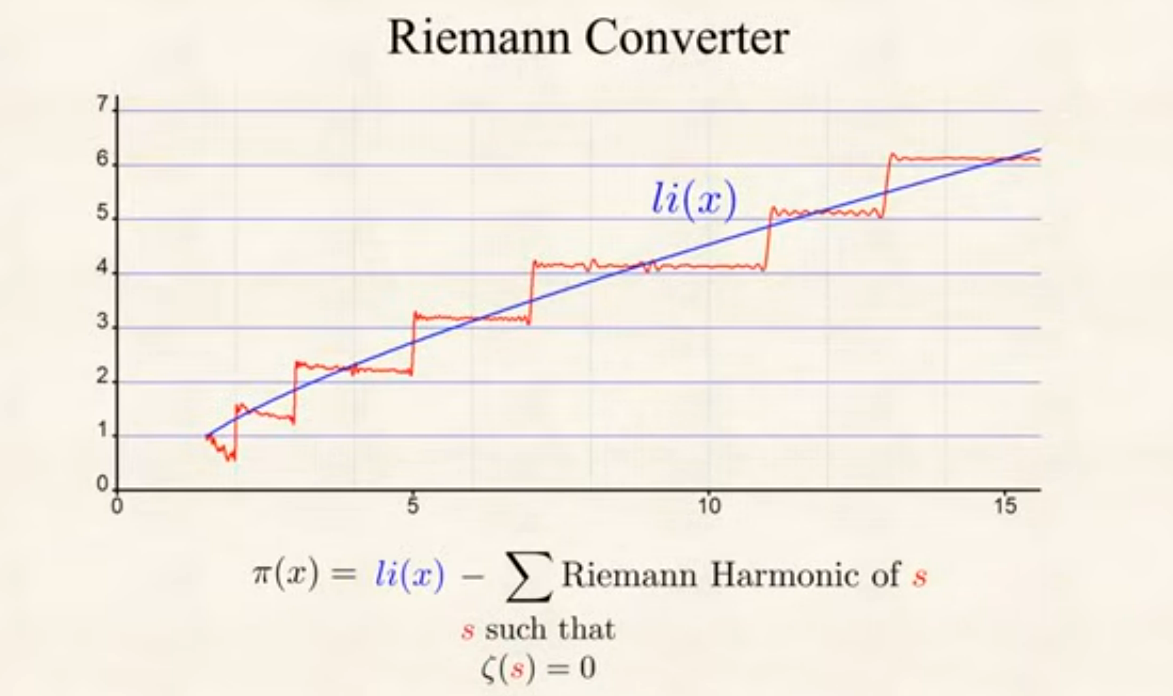
That is, the prime counting function is approximately equal to the logarithmic integral and the correcting terms are given by the Riemann harmonics of the nontrivial zeroes of the Riemann zeta function.

In a more formal approach, there is an “exact” formula, due to Riemann, which expresses $\pi (x)$ in terms of the non‑trivial zeros $\rho$ of $\zeta (s)$. One convenient form is via the so‑called Riemann–von Mangoldt explicit formula for the weighted counting function

namely

where

• the sum runs over all non‑trivial zeros $\rho$ of $\zeta (s)$,
• ${\displaystyle \mathrm{Li}(x)={\int }_2^x\frac{dt}{\ln t}}$ is the logarithmic integral.

Then one inverts the relation $J(x)=\sum _{n\ge 1}\pi (x^{1/n})/n$ by Möbius inversion to recover $\pi (x)$:

where $\mu$ is the Möbius function.

Hence, although there is no elementary “closed‑form” for $\pi (x)$, the above gives an exact representation in terms of the non‑trivial zeros of $\zeta (s)$.