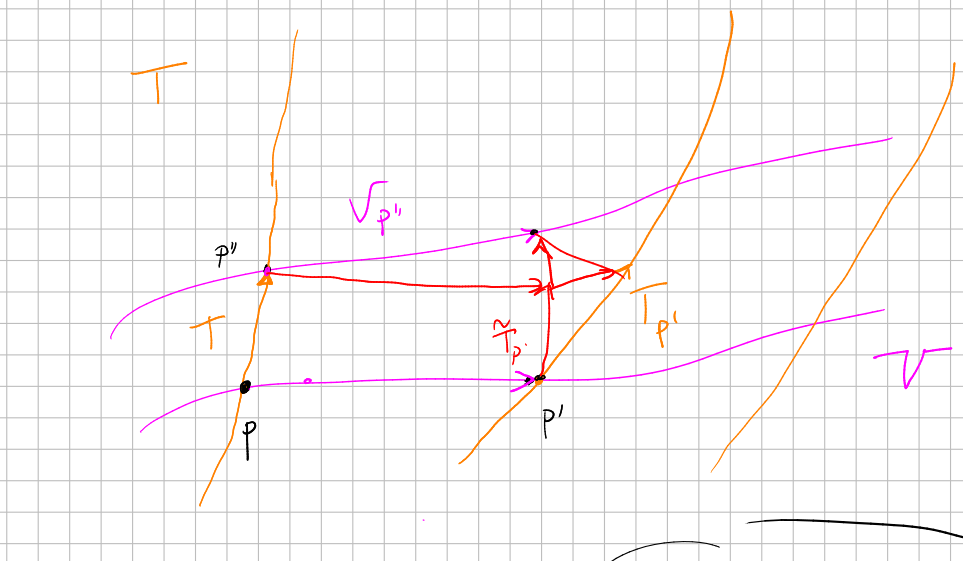
Relation between Lie derivative and covariant derivative

Better explanation in this video made by myself.

In both cases we want to understand the derivatives as the velocity of curves in the same finite dimensional vector space . But the approach is different:

• In the case of ${\mathcal{L}}_{V}T$, we use the flow ${\phi }_V^t$ of $V$. So the curve is $t\mapsto {\phi }_{V,\star }^{-t}(T({\phi }_V^t(x)))$. We could write, informally, that

when we go from a point $p$ to a near point $p^{\prime }$, being ${\hat{T}}_{p^{\prime }}$ "what $T_{p^{\prime }}$ should be", i.e., the pushforward of $T_p$ by means of the flow of $V$. See Lie derivative of vector fields#Personal interpretation.

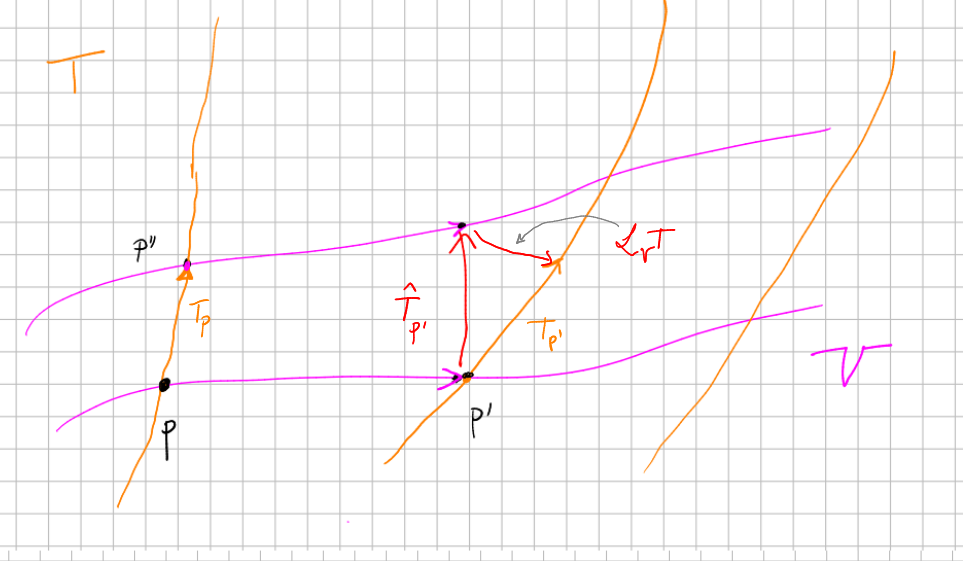
• In the case of ${\mathrm{\nabla }}_{v}T$, we use the parallel transport ${\mathrm{\Pi }}_{\eta ,t}$ along $\eta$ with respect to $\mathrm{\nabla }$. So the curve is $t\mapsto {\mathrm{\Pi }}_{\eta ,t}^{-1}(T(\eta (t)))$. (Here $\eta$ denotes any smooth curve passing through $x$ at $t=0$ with velocity $v$, and ${\mathrm{\Pi }}_{\eta ,t}:T_{x}M\to T_{\eta (t)}M$)
  We could write, informally, that

when we go from a point $p$ to a near point $p^{\prime }$. The expression ${\tilde{T}}_{p^{\prime }}$ means what $T_{p^{\prime }}$ should be, i.e., the parallel transport (which depends on the geometry) of $T_p$ along $V$.

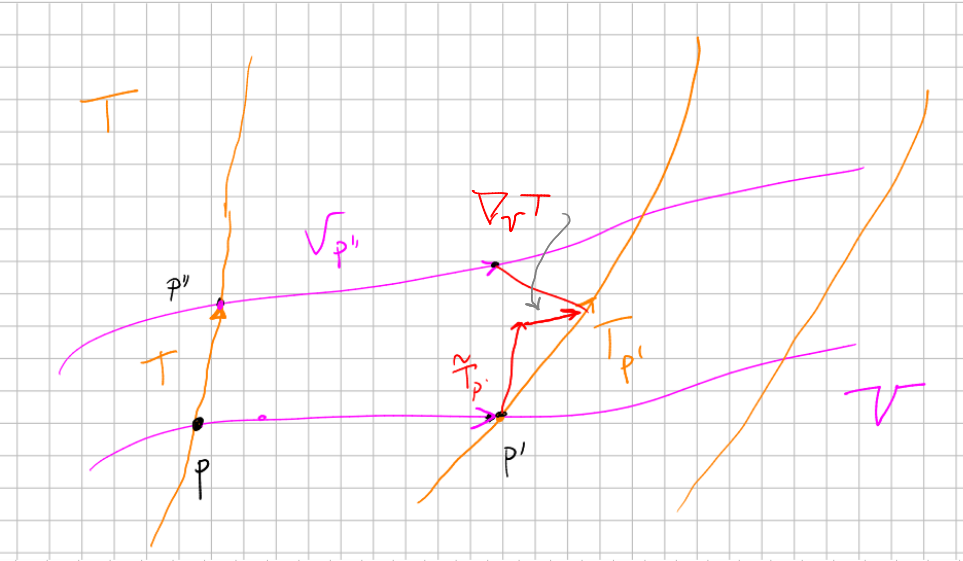
Finally, since the torsion of a connection is the fail to close a parallelogram made of parallel transported vectors, we have the following computational relation between covariant derivatives and Lie derivatives:

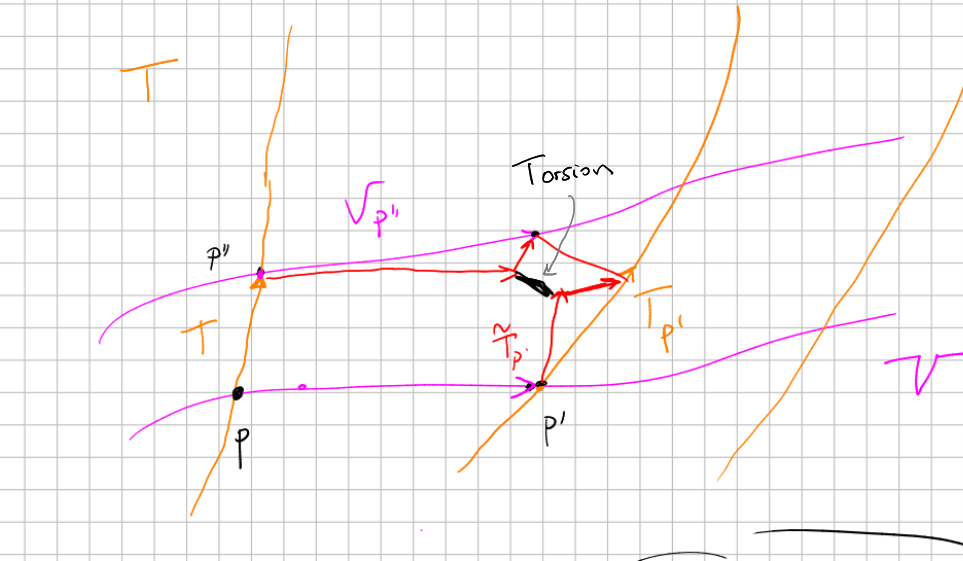
Also, most connections are torsion free, and in those cases we have: